Question

【题目】“作差法”是常见的比较代数式大小的一种方法，即要比较代数式M、N的大小，只要作出它们的差M﹣N，若M﹣N＞0，则M＞N；若M﹣N=0，则M=N；若M﹣N＜0，则M＜N．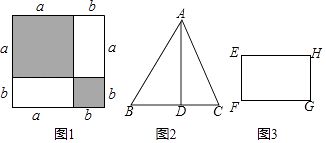

（1）如图1，把边长为a+b（a≠b）的大正方形分割成两个边长分别是a、b的小正方形及两个长方形，试比较来两个小正方形面积之和M与两个长方形面积之和N的大小．
（2）如图2，图3，△ABC中，AD⊥BC于D，AD=BC=2x﹣y，长方形EFGH中，长EH=2x﹣ y，宽EF=y，△ABC与长方形EFGH的面积分别为M、N，试比较M、N的大小，其中y＞0，x＞ y且x≠y．

Answer 1

【答案】
（1）

解：根据题意得：M=a2+b2，N=ab+ab，

∴M﹣N=a2+b2﹣2ab=（a﹣b）2＞0，

∴a≠b，

∴（a﹣b）2＞0，

∴M﹣N＞0，

∴M＞N

（2）

解：在△ABC中，AD⊥BC于D，AD=BC=2x﹣y，

∴M= BCAD

= （2x﹣y）2

=2x2﹣2xy+ y2，

在长方形EFGH中，长EH=2x﹣ y，宽EF=y，

∴N=EHEF

=（2x﹣ y）y

=2xy﹣ y2，

∴M﹣N=（2x2﹣2xy+ y2）﹣（2xy﹣ y2）

=2x2﹣2xy+ y2﹣2xy+ y2

=2x2﹣4xy+2y2

=2（x2﹣2xy+y2）

=2（x﹣y）2，

∵x≠y，

∴（x﹣y）2＞0，

∴2（x﹣y）2＞0，

∴M﹣N＞0，

即：M＞N．

【解析】【解决问题】利用作差法比较M与N大小即可；【拓展延伸】利用作差法比较M与N大小即可；
【考点精析】本题主要考查了平行四边形的性质和平行四边形的判定的相关知识点，需要掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分；两组对边分别平行的四边形是平行四边形：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形才能正确解答此题．