【题目】已知关于x的分式方程 ![]() +
+ ![]() =1(a≠2且a≠3)的解为正数,求字母a的取值范围.
=1(a≠2且a≠3)的解为正数,求字母a的取值范围.
参考答案:
【答案】解:方程两边都乘以x(x﹣1),得 x2+2﹣a=x2﹣x,
解得x=2﹣a,
由分式有意义,得
2﹣a≠1,2﹣a≠0,
解得a≠3,a≠2.
由关于x的分式方程 ![]() +
+ ![]() =1(a≠2且a≠3)的解为正数,得
=1(a≠2且a≠3)的解为正数,得
2﹣a>0,
解得a<2,
字母a的取值范围a<2
【解析】根据等式的性质,可得整式方程,根据解整式方程,可得x,根据解为正数,可得关于a的不等式,根据解不等式,可得答案.
【考点精析】根据题目的已知条件,利用分式方程的解和一元一次不等式的解法的相关知识可以得到问题的答案,需要掌握分式方程无解(转化成整式方程来解,产生了增根;转化的整式方程无解);解的正负情况:先化为整式方程,求整式方程的解;步骤:①去分母;②去括号;③移项;④合并同类项; ⑤系数化为1(特别要注意不等号方向改变的问题).
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题 八年级学生去距学校10km的博物馆参观,一部分学生骑自行车先走,过了20min后,其余学生乘汽车出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度.
-
科目: 来源: 题型:
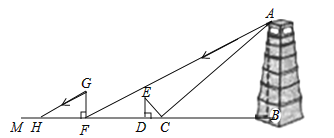
查看答案和解析>>【题目】某市为了打造森林城市,树立城市新地标,实现绿色、共享发展理念,在城南建起了“望月阁”及环阁公园.小亮、小芳等同学想用一些测量工具和所学的几何知识测量“望月阁”的高度,来检验自己掌握知识和运用知识的能力.他们经过观察发现,观测点与“望月阁”底部间的距离不易测得,因此经过研究需要两次测量,于是他们首先用平面镜进行测量.方法如下:如图,小芳在小亮和“望月阁”之间的直线BM上平放一平面镜,在镜面上做了一个标记,这个标记在直线BM上的对应位置为点C,镜子不动,小亮看着镜面上的标记,他来回走动,走到点D时,看到“望月阁”顶端点A在镜面中的像与镜面上的标记重合,这时,测得小亮眼睛与地面的高度ED=1.5米,CD=2米,然后,在阳光下,他们用测影长的方法进行了第二次测量,方法如下:如图,小亮从D点沿DM方向走了16米,到达“望月阁”影子的末端F点处,此时,测得小亮身高FG的影长FH=2.5米,FG=1.65米.
如图,已知AB⊥BM,ED⊥BM,GF⊥BM,其中,测量时所使用的平面镜的厚度忽略不计,请你根据题中提供的相关信息,求出“望月阁”的高AB的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.等腰梯形B.平行四边形C.正三角形D.圆
-
科目: 来源: 题型:
查看答案和解析>>【题目】有五条线段,长度分别是2,4,6,8,10,从中任取三条能构成三角形的概率是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,D、E分别是AB、AC的中点,连DE,若DE=6,则BC的长是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“作差法”是常见的比较代数式大小的一种方法,即要比较代数式M、N的大小,只要作出它们的差M﹣N,若M﹣N>0,则M>N;若M﹣N=0,则M=N;若M﹣N<0,则M<N.
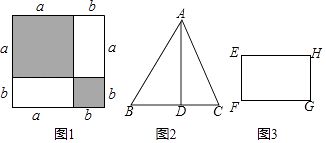
(1)如图1,把边长为a+b(a≠b)的大正方形分割成两个边长分别是a、b的小正方形及两个长方形,试比较来两个小正方形面积之和M与两个长方形面积之和N的大小.
(2)如图2,图3,△ABC中,AD⊥BC于D,AD=BC=2x﹣y,长方形EFGH中,长EH=2x﹣ y,宽EF=y,△ABC与长方形EFGH的面积分别为M、N,试比较M、N的大小,其中y>0,x>
y,宽EF=y,△ABC与长方形EFGH的面积分别为M、N,试比较M、N的大小,其中y>0,x>  y且x≠y.
y且x≠y.
相关试题

