【题目】阅读下面材料:
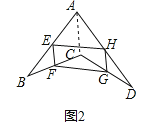
在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?
小敏在思考问题时,有如下思路:连接AC.

结合小敏的思路作答:
(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由,参考小敏思考问题的方法解决一下问题;
(2)如图2,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;
②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.

参考答案:
【答案】(1)是平行四边形;(2)①AC=BD;②AC⊥BD.
【解析】
试题分析:(1)如图2,连接AC,根据三角形中位线的性质及平行四边形判定定理即可得到结论;
(2)①由(1)知,四边形EFGH是平行四边形,且FG=![]() BD,HG=
BD,HG=![]() AC,于是得到当AC=BD时,FG=HG,即可得到结论;
AC,于是得到当AC=BD时,FG=HG,即可得到结论;
②若四边形EFGH是矩形,则∠HGF=90°,即GH⊥GF,又GH∥AC,GF∥BD,则AC⊥BD.
试题解析:(1)是平行四边形.证明如下:
如图2,连接AC,∵E是AB的中点,F是BC的中点,∴EF∥AC,EF=![]() AC,同理HG∥AC,HG=
AC,同理HG∥AC,HG=![]() AC,综上可得:EF∥HG,EF=HG,故四边形EFGH是平行四边形;
AC,综上可得:EF∥HG,EF=HG,故四边形EFGH是平行四边形;
(2)①AC=BD.
理由如下:
由(1)知,四边形EFGH是平行四边形,且FG=![]() BD,HG=
BD,HG=![]() AC,∴当AC=BD时,FG=HG,∴平行四边形EFGH是菱形;
AC,∴当AC=BD时,FG=HG,∴平行四边形EFGH是菱形;
②当AC⊥BD时,四边形EFGH为矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下问题,不适合用普查的是( )
A. 了解全班同学每周阅读的时间B. 亚航客机飞行前的安全检测
C. 了解全市中小学生每天的零花钱D. 某企业招聘部门经理,对应聘人员面试
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数中,不相等的一组是( )
A. (-2)3和-23 B. (-2)2和-22
C. +(-2)和-2 D. |-2|3和|2|3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(
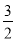 ,0),B(0,2),则点B2016的坐标为______________.
,0),B(0,2),则点B2016的坐标为______________.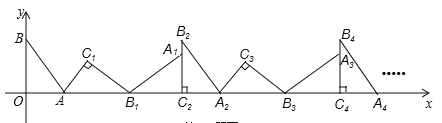
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BD是矩形ABCD的对角线.

(1)用直尺和圆规作线段BD的垂直平分线,分别交AD、BC于E、F(保留作图痕迹,不写作法和证明).
(2)连结BE,DF,问四边形BEDF是什么四边形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,对于任意两点A(x1,y1)B (x2,y2),规定运算:
(1)A⊕B=(x1+x2,y1+y2);
(2)A⊙B=x1x2+y1y2;
(3)当x1=x2且y1=y2时,A=B.
有下列四个命题:
①若有A(1,2),B(2,﹣1),则A⊕B=(3,1),A⊙B=0;
②若有A⊕B=B⊕C,则A=C;
③若有A⊙B=B⊙C,则A=C;
④(A⊕B)⊕C=A⊕(B⊕C)对任意点A、B、C均成立.
其中正确的命题为______(只填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列有关圆的一些结论:①与半径长相等的弦所对的圆周角是30°;②圆内接正六边形的边长与该圆半径相等;③垂直于弦的直径平分这条弦;④平分弦的直径垂直于弦.其中正确的是( )
A. ①②③ B. ①③④ C. ②③ D. ②④
相关试题

