【题目】某运动队欲从甲、乙两名优秀选手中选一名参加全省射击比赛,该运动队预先对这两名选手进行了8次测试,测得的成绩如表:
次数 | 选手甲的成绩(环) | 选手乙的成绩(环) |
1 | 9.6 | 9.5 |
2 | 9.7 | 9.9 |
3 | 10.5 | 10.3 |
4 | 10.0 | 9.7 |
5 | 9.7 | 10.5 |
6 | 9.9 | 10.3 |
7 | 10.0 | 10.0 |
8 | 10.6 | 9.8 |
根据统计的测试成绩,请你运用所学过的统计知识作出判断,派哪一位选手参加比赛更好?为什么?
参考答案:
【答案】派乙选手参加比赛更好
【解析】
试题分析:根据平均数的计算公式先分别求出甲和乙的平均数,再根据方差公式进行计算即可得出答案.
解:∵甲的平均数是:![]() (9.6+9.7+…+10.6)=10,
(9.6+9.7+…+10.6)=10,
乙的平均数是:![]() (9.5+9.9+…+9.8)=10,
(9.5+9.9+…+9.8)=10,
∴S2甲=![]() [(9.6﹣10)2+(9.7﹣10)2+…+(10.6﹣10)2]=0.12,
[(9.6﹣10)2+(9.7﹣10)2+…+(10.6﹣10)2]=0.12,
S2乙=![]() [(9.5﹣10)2+(9.9﹣10)2+…+(9.8﹣10)2]=0.1025,
[(9.5﹣10)2+(9.9﹣10)2+…+(9.8﹣10)2]=0.1025,
∵S2甲>S2乙,
∴派乙选手参加比赛更好.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果△+△=*,○+○=◆,△=○+○+○+○,那么*+◆= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,半径为1的⊙A的圆心与坐标原点O重合,线段BC的端点分别在x轴与y轴上,点B的坐标为(6,0),且sin∠OCB=
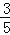 .
.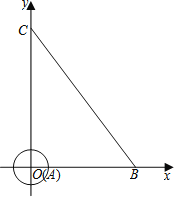
(1)若点Q是线段BC上一点,且点Q的横坐标为m.
①求点Q的纵坐标;(用含m的代数式表示)
②若点P是⊙A上一动点,求PQ的最小值;
(2)若点A从原点O出发,以1个单位/秒的速度沿折线OBC运动,到点C运动停止,⊙A随着点A的运动而移动.
①点A从O→B的运动的过程中,若⊙A与直线BC相切,求t的值;
②在⊙A整个运动过程中,当⊙A与线段BC有两个公共点时,直接写出t满足的条件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
填空:①∠AEB的度数为 ;②线段AD,BE之间的数量关系为 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图表示两辆汽车行驶路程与时间的关系(汽车B在汽车A后出发)的图象,试回答下列问题:

(1)图中l1,l2分别表示哪一辆汽车的路程与时间的关系?
(2)写出汽车A和汽车B行驶的路程s与时间t的函数关系式,并求汽车A和汽车B的速度;
(3)图中交点的实际意义是什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=3,点D为AC边上的动点,点D从点C出发,沿边CA向A运动,当运动到点A时停止,若设点D运动的速度为每秒1个单位长度,当运动时间t为多少秒时,以点C、B、D为顶点的三角形是等腰三角形?
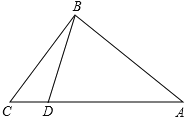
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC且BD>CD,DF⊥AB,△CDE和△ADB都是等腰直角三角形,给出下列结论,正确的是
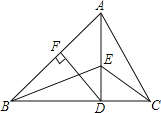
①△ADC≌△BDE;
②△ADF≌△BDF;
③△CDE≌△AFD;
④△ACE≌ABE.
相关试题

