【题目】如图,在平面直角坐标系中,半径为1的⊙A的圆心与坐标原点O重合,线段BC的端点分别在x轴与y轴上,点B的坐标为(6,0),且sin∠OCB=![]() .
.
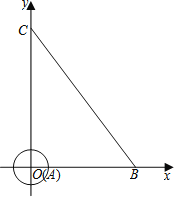
(1)若点Q是线段BC上一点,且点Q的横坐标为m.
①求点Q的纵坐标;(用含m的代数式表示)
②若点P是⊙A上一动点,求PQ的最小值;
(2)若点A从原点O出发,以1个单位/秒的速度沿折线OBC运动,到点C运动停止,⊙A随着点A的运动而移动.
①点A从O→B的运动的过程中,若⊙A与直线BC相切,求t的值;
②在⊙A整个运动过程中,当⊙A与线段BC有两个公共点时,直接写出t满足的条件.
参考答案:
【答案】(1)①﹣![]() m+8;②PQ最小=OQ最小﹣1=3.8;(2)①t=
m+8;②PQ最小=OQ最小﹣1=3.8;(2)①t=![]() 时,⊙A与直线BC相切;②
时,⊙A与直线BC相切;②![]() <t≤5或7≤t≤15时,⊙A与线段BC有两个公共点.
<t≤5或7≤t≤15时,⊙A与线段BC有两个公共点.
【解析】
试题分析:(1)①根据正切的概念求出BC=10,OC=8,运用待定系数法求出直线BC的解析式,根据函数图象上点的坐标特征解得即可;
②作OQ⊥AB交⊙A于P,则此时PQ最小,根据三角形面积公式计算即可;
(2)①根据切线的性质和相似三角形的性质计算即可;
②结合图形、运用直线与圆的位置关系定理解答.
解:(1)①∵点B的坐标为(6,0),tan∠OCB=![]() ,
,
∴BC=10,OC=8,
设直线BC的解析式为y=kx+b,
![]() ,
,
解得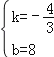 ,
,
∵点Q的横坐标为m,
∴点Q的纵坐标为﹣![]() m+8;
m+8;
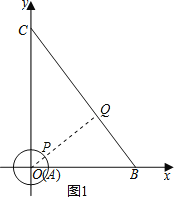
②如图1,作OQ⊥AB交⊙A于P,则此时PQ最小,
![]() ×AB×OQ=
×AB×OQ=![]() ×BO×CO,
×BO×CO,
解得,OQ=4.8,
∴PQ最小=OQ最小﹣1=3.8;
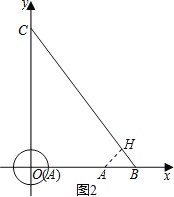
(2)①如图2,⊙A与直线BC相切于H,
则AH⊥BC,又∠BOC=90°,
∴△BHA∽△BOC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,BA=![]() ,
,
则OA=6﹣![]() =
=![]() ,
,
∴t=![]() 时,⊙A与直线BC相切;
时,⊙A与直线BC相切;
②由(2)①得,t=![]() 时,⊙A与直线BC相切,
时,⊙A与直线BC相切,
当t=5时,⊙A经过点B,
当t=7时,⊙A经过点B,
当t=15时,⊙A经过点C,
故![]() <t≤5或7≤t≤15时,⊙A与线段BC有两个公共点.
<t≤5或7≤t≤15时,⊙A与线段BC有两个公共点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AB的垂直平分线DE交AC于D,垂足为E,若∠A=30°,CD=3.

(1)求∠BDC的度数.
(2)求AC的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O是坐标原点,二次函数y=x2+c的图象抛物线交x轴于点A,B(点A在点B的左侧),与y轴交于点C(0,﹣3).
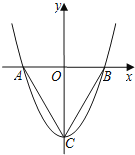
(1)求∠ABC的度数;
(2)若点D是第四象限内抛物线上一点,△ADC的面积为
 ,求点D的坐标;
,求点D的坐标;(3)若将△OBC绕平面内某一点顺时针旋转60°得到△O′B′C′,点O′,B′均落在此抛物线上,求此时O′的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果△+△=*,○+○=◆,△=○+○+○+○,那么*+◆= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
填空:①∠AEB的度数为 ;②线段AD,BE之间的数量关系为 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某运动队欲从甲、乙两名优秀选手中选一名参加全省射击比赛,该运动队预先对这两名选手进行了8次测试,测得的成绩如表:
次数
选手甲的成绩(环)
选手乙的成绩(环)
1
9.6
9.5
2
9.7
9.9
3
10.5
10.3
4
10.0
9.7
5
9.7
10.5
6
9.9
10.3
7
10.0
10.0
8
10.6
9.8
根据统计的测试成绩,请你运用所学过的统计知识作出判断,派哪一位选手参加比赛更好?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图表示两辆汽车行驶路程与时间的关系(汽车B在汽车A后出发)的图象,试回答下列问题:

(1)图中l1,l2分别表示哪一辆汽车的路程与时间的关系?
(2)写出汽车A和汽车B行驶的路程s与时间t的函数关系式,并求汽车A和汽车B的速度;
(3)图中交点的实际意义是什么?
相关试题

