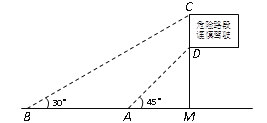
【题目】如图,为了测量矗立在高速公路水平地面上的交通警示牌的高度CD,在距M相距4米的A处,测得警示牌下端D的仰角为45°,再笔直往前走8米到达B处,在B处测得警示牌上端C的仰角为30°,求警示牌的高度CD.(结果精确到0.1米,参考数据:![]() ,
,![]() )
)
参考答案:
【答案】警示牌的高度CD约为2.9米.
【解析】试题分析:先在Rt△ADM中,根据AM=4,∠MAD=45°求出DM=4;在Rt△BCM中,根据∠MBC=30°,BM=12求出CM的值,再根据CD=MC-DM计算即可;
试题解析:
在Rt△ADM中,
∵AM=4,∠MAD=45°,
∴DM =AM =4,
∵AB=8,
∴MB=AM+AB=12,
在Rt△BCM中,
∵∠MBC=30°,
∴MC=MBtan30°=![]() ,
,
∴DC= MC - DM =![]() (米),
(米),
答:警示牌的高度CD约为2.9米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(21+2)÷(-23)= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】-6×0÷10=.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a+b+1=0,则3a2+3b2+6ab的值是( )
A. 1 B. -1 C. 3 D. -3
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题。
(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.
证明:DE=BD+CE.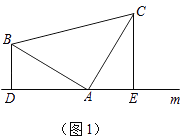
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.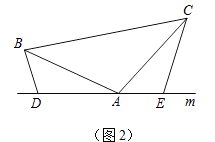
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.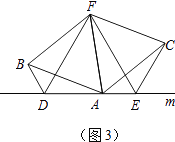
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中, AC=6, BC=4.
(1)用直尺和圆规作∠ACB的角平分线CD,交AB于点D;
(保留作图痕迹,不要求写作法和证明)
(2)在(1)所作的图形中,若△ACD的面积为3,求△BCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,EG∥AF,请你从下面三个条件中,再选出两个作为已知条件,另一个作为结论,推出一个正确的命题.并证明这个命题(只写出一种情况)①AB=AC ②DE=DF ③BE=CF
已知:EG∥AF, , .
求证: .
证明:
相关试题

