【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.

(1)试判断线段AB与AC的数量关系,并说明理由;
(2)若![]() ,求⊙O的半径和线段PB的长.
,求⊙O的半径和线段PB的长.
参考答案:
【答案】(1)AB=AC;(2)圆的半径是3,线段PB的长为![]() .
.
【解析】
试题分析:(1)连接OB,根据切线的性质和垂直的定义得出∠OBA=∠OAC=90°,推出∠OBP+∠ABP=90°,∠ACP+∠CPA=90°,求出∠ACP=∠ABC,根据等腰三角形的判定推出即可;
(2)延长AP交⊙O于D,连接BD,设圆半径为r,则OP=OB=r,PA=5﹣r,根据AB=AC推出52﹣r2=(2![]() )2﹣(5﹣r)2,求出r,证△DPB∽△CPA,得出关于BP的比例式,代入求出即可.
)2﹣(5﹣r)2,求出r,证△DPB∽△CPA,得出关于BP的比例式,代入求出即可.
解:(1)AB=AC,理由如下:
连接OB.
∵AB切⊙O于B,OA⊥AC,
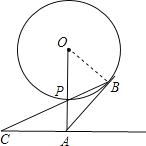
∴∠OBA=∠OAC=90°,
∴∠OBP+∠ABP=90°,∠ACP+∠APC=90°,
∵OP=OB,
∴∠OBP=∠OPB,
∵∠OPB=∠APC,
∴∠ACP=∠ABC,
∴AB=AC;
(2)延长AP交⊙O于D,连接BD,
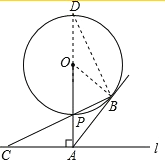
设圆半径为r,则OP=OB=r,PA=5﹣r,
则AB2=OA2﹣OB2=52﹣r2,
AC2=PC2﹣PA2=(2![]() )2﹣(5﹣r)2,
)2﹣(5﹣r)2,
∴52﹣r2=(2![]() )2﹣(5﹣r)2,
)2﹣(5﹣r)2,
解得:r=3,
∴AB=AC=4,
∵PD是直径,
∴∠PBD=90°=∠PAC,
又∵∠DPB=∠CPA,
∴△DPB∽△CPA,
∴![]() ,
,
∴![]() ,
,
∴BP=![]() ,
,
答:圆的半径是3,线段PB的长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用不等式表示:x的两倍与3的差不小于5,则这个不等式是_______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某酒店有三人间、双人间客房若干,各种房型每天的收费标准如下:
普通(元/间)
豪华(元/间)
三人间
160
400
双人间
140
300
一个50人的旅游团到该酒店入住,选择了一些三人普通间和双人豪华间入住,且恰好住满.已知该旅游团当日住宿费用共计4020元,问该旅游团入住的三人普通间和双人豪华间各为几间?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某人骑自行车从甲地到乙地,到达乙地他马上返回甲地.如图反映的是他离甲地的距离s(km)及他骑车的时间t(h)之间的关系,则下列说法正确的是( )
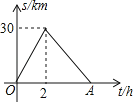
A.甲、乙两地之间的距离为60km
B.他从甲地到乙地的平均速度为30km/h
C.当他离甲地15km时,他骑车的时间为1h
D.若他从乙地返回甲地的平均速度为10km/h,则点A表示的数字为5
-
科目: 来源: 题型:
查看答案和解析>>【题目】本学期初,我市教育部门对某中学从学生的品德、身心、学习、创新、国际、审美、信息、生活八个方面进行了综合评价,评价小组从八年级学生中选取部分学生针对“信息素养”进行测试,并将测试结果绘制成如下统计图(如图).根据图中信息,解答下列问题:
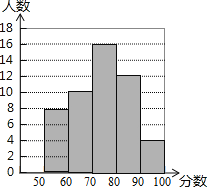
(1)本次选取参加测试的学生人数是 ;
(2)学生“信息素养”得分的中位数是 ;
(3)若把每组中各个分数用这组数据的中间值代替(如30﹣40分的中间值为35分),则参加测试的学生的平均分为 分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】E、F、G、H分别是四边形ABCD四条边的中点,要使四边形EFGH为矩形,四边形ABCD应具备的条件是( )
A、对角线相等
B、一组对边平行而另一组对边不平行
C、对角线互相垂直
D、对角线互相平分
-
科目: 来源: 题型:
查看答案和解析>>【题目】毕达哥拉斯学派对”数”与”形”的巧妙结合作了如下研究:
名称及图形
几何点数
层数
三角形数
正方形数
五边形数
六边形数




第一层几何点数
1
1
1
1
第二层几何点数
2
3
4
5
第三层几何点数
3
5
7
9
…
…
…
…
…
第六层几何点数
…
…
…
…
…
第n层几何点数
请写出第六层各个图形的几何点数,并归纳出第n层各个图形的几何点数.
相关试题

