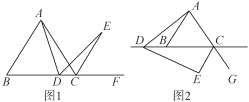
【题目】如图1,△ABC为等边三角形,D为BC上任一点,∠ADE=60°,边DE与∠ACB外角的平分线相交于点E.
(1)求证:AD=DE.
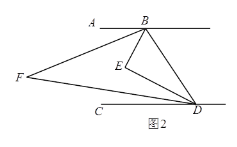
(2)若点D在CB的延长线上,如图2,(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由.
参考答案:
【答案】(1)证明见解析;(2)成立,证明见解析.
【解析】
(1)在AB上取一点M,使BM=BD,连接MD.则△BDM是等边三角形,则易证AM=DC,根据ASA即可证得△AMD≌△DCE(ASA),根据全等三角形的对应边相等,即可证得;
(2)延长CA到M,使AM=BD,与(1)相同,可证△CDM是等边三角形,然后证明△AMD≌△ECD(ASA),根据全等三角形的对应边相等,即可证得.
(1)证明:如图1,在AB上取一点M,使BM=BD,连接MD.
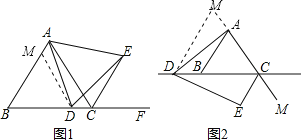
∵△ABC是等边三角形,
∴∠B=60°,BA=BC.
∴△BMD是等边三角形,∠BMD=60°.∠AMD=120°.
∵CE是外角∠ACF的平分线,
∴∠ECF=60°,∠DCE=120°.
∴∠AMD=∠DCE.
∵∠ADE=∠B=60°,∠ADC=∠CDE+∠ADE=∠MAD+∠B,
∴∠CDE=∠MAD.
又∵BA-BM=BC-BD,即MA=CD.
在△AMD和△DCE中,
 ,
,
∴△AMD≌△DCE(ASA),
∴AD=DE.
(2)答:正确.
证明:延长CA到M,使AM=BD,与(1)相同,可证△CDM是等边三角形,
∴∠CDM=∠M=60°,CD=DM,
∵∠ADE=60°,
∴∠ADM=∠EDC,
在△AMD和△DCE中,
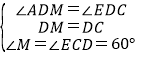 ,
,
∴△AMD≌△ECD(ASA),
∴AD=DE.
-
科目: 来源: 题型:
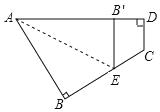
查看答案和解析>>【题目】如图所示,一个四边形纸片 ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点 B 落在 AD 边上的 B′点,AE 是折痕.
(1)试判断 B′E 与 DC 的位置关系,并说明理由;
(2)如果∠C=128°,求∠AEB 的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC在网格中(网格中每个小正方形的边长均为1)依次进行位似变换、轴对称变换和平移变换后得到△A3B3C3 .

(1)△ABC与△A1B1C1的位似比等于;
(2)在网格中画出△A1B1C1关于y轴的轴对称图形△A2B2C2;
(3)请写出△A3B3C3是由△A2B2C2怎样平移得到的?
(4)设点P(x,y)为△ABC内一点,依次经过上述三次变换后,点P的对应点的坐标为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC中,D、E、F三点分别在AB,AC,BC三边上,过点D的直线与线段EF的交点为点H,∠1+∠2=180°,∠3=∠C.
(1)求证:DE∥BC;
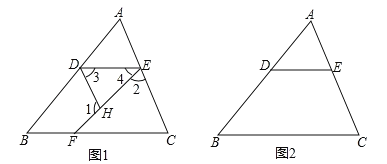
(2)在以上条件下,若△ABC及D,E两点的位置不变,点F在边BC上运动使得∠DEF的大小发生变化,保证点H存在且不与点F重合,探究:要使∠1=∠BFH成立,请说明点F应该满足的位置条件,在图2中画出符合条件的图形并说明理由.
(3)在(2)的条件下,若∠C=α,直接写出∠BFH的大小 .
-
科目: 来源: 题型:
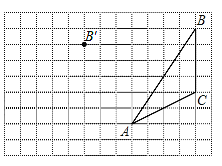
查看答案和解析>>【题目】画图并填空:如图,方格纸中每个小正方形的边长都为 1,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B 的对应点 B′.
(1)在给定方格纸中画出平移后的△A′B′C′;
(2)线段 AA′与线段 BB′的数量和位置关系是___________;
(3)求△A′B′C′的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年3月全国两会胜利召开,某数学兴趣小组就两会期间出现频率最高的热词:A脱贫攻坚.B.绿色发展.C.自主创新.D.简政放权等热词进行了抽样调查,每个同学只能从中选择一个“我最关注”的热词,如图是根据调查结果绘制的两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题: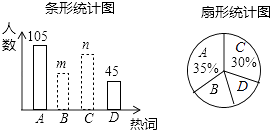
(1)本次调查中,一共调查了名同学;
(2)条形统计图中,m= , n=;
(3)扇形统计图中,热词B所在扇形的圆心角的度数是;
(4)从该校学生中随机抽取一个最关注热词D的学生的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知BE平分∠ABD,DE平分∠BDC,且∠BED =∠ABE +∠EDC.
(1)如图1,求证:AB//CD;
(2)如图2,若∠ABE=3∠ABF,且∠BFD=30°时,试求
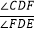 的值;
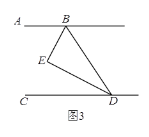
的值;(3)如图3,若H是直线CD上一动点(不与D重合),BI平分∠HBD,画出图形,并探究出∠EBI与∠BHD的数量关系.
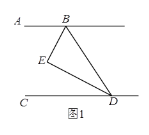
相关试题

