【题目】如图,在四边形ACBM中,∠C=∠M=90°,∠CAB=∠MAB=60°,将△ABM绕点A顺时针旋转α(α<∠BAC),得到Rt△ADE,其中斜边AE交BC于点F,直角边DE分别交AB,BC于点G,H.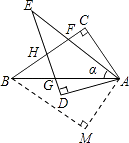
(1)求证:△ACB≌△AMB;
(2)若α=30°,求证:四边形ADHC是正方形;
(3)若∠AFG=70°,求α的值.
参考答案:
【答案】
(1)
证明:△ACB与△AMB中,
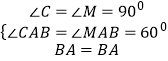 ,
,
∴△ACB≌△AMB(AAS)
(2)
证明:当α=30°时,∠MAD=30°,
∵∠CAB=∠MAB=60°,
∴∠GAD=30°,
∴∠CAD=90°.
∴四边形ADHC是矩形.
∵△ACB≌△AMB,
∴AC=AM=AD,
∴四边形ADHC是正方形
(3)
解:如图,
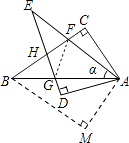
连接FG,
∵∠CAF+∠FABF=∠GAD+∠FAB,
∴∠CAF=∠GAD,
在△ACF和△ADG中,
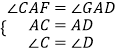 ,
,
∴△ACF≌△ADG(ASA),
∴AF=AG,
∴∠AGF=∠AFG=70°,
∴α=40°.
【解析】(1)根据已知利用全等三角形的判定定理AAS定理可得结论;(2)由旋转可知∠MAD=30°,利用角的加减可得∠GAD=30°,易得∠CAD=90°,又因为∠C=∠D=90°,由矩形的判定定理可知四边形ADHC是矩形,由全等三角形的性质和旋转的性质可得AC=AD,利用正方形的判定定理可得结论;(3)连接FG,利用全等三角形的性质和旋转的性质可得∠CAB=∠DAE,易得∠CAF=∠ADG,易得△ACF≌△ADG,由全等三角形的性质定理可得AF=AG,利用三角形的内角和定理可得结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B为反比例函数
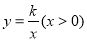 图像上的两点,A、B两点坐标分别为(
图像上的两点,A、B两点坐标分别为(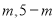 )、(
)、(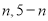 )(m<n),连接AB并延长交
)(m<n),连接AB并延长交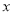 轴于点C.
轴于点C.(1)求
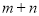 的值;
的值;(2)若B为AC的中点,求
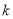 的值;
的值;(3)过B点作OA的平行线交
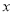 轴于(
轴于(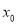 ,0),若
,0),若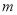 为整数,求
为整数,求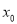 值.
值. 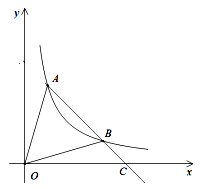
-
科目: 来源: 题型:
查看答案和解析>>【题目】DNA分子直径为0.00000069cm,则这个数用科学记数法表示为:_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BD=BC=30m.
(1)求∠ADC的度数;
(2)求A、D两地的距离.

-
科目: 来源: 题型:
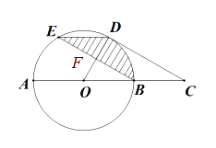
查看答案和解析>>【题目】如图,在⊙O中,AB是直径,D、E为⊙O上两点,过点D作⊙O的切线CD交AB的延长线于点C,OD与BE交于F点,四边形BCDE是平行四边形.
(1)求证:四边形AODE是平行四边形.;
(2)若⊙O的半径为6,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“先看到闪电,后听到雷声”,那是因为在空气中光的传播速度比声音快.科学家发现,光在空气里的传播速度约为3×108米/秒,而声音在空气里的传播速度大约为3×102米/秒.在空气中光的速度是声速的_____倍.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简与求值:
(1)化简:[(a+b)(a﹣b)﹣(a﹣b)2]+2b(a+b)
(2)已知:16×2m+1=29,求m的值.
相关试题

