Question

【题目】请认真观察图形，解答下列问题：

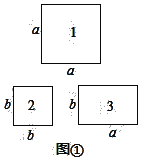
如图①，1号卡片是边长为a的正方形，2号卡片是边长为b的正方形，3号卡片是一个长和宽分别为a，b的长方形．

（1）若选取1号、2号、3号卡片分别为1张、1张、2张，可拼成一个正方形，如图②，能用此图解释的乘法公式是______________；（请用字母a，b表示）

（2）若选取1号、2号、3号卡片分别为1张、2张、3张，可拼成一个长方形（不重叠无缝隙），则能用此图解释的整式乘法运算是____________________；（请画出图形，并用字母a，b表示）

（3）如果图中的a，b（a＞b）满足a2+b2=57，ab=12，求a+b的值；

（4）已知（5+2x）2+（3+2x）2=60，求（5+2x）（2x+3）的值．

Answer 1

【答案】 （a+b）2=a2+2ab+b2 （a+b）（a+2b）=a2+3ab+2b2

【解析】（1）由图中正方形的面积=中间的各图片的面积的和，就可得出代数式．即（a+b）2=a2+2ab+b2；

（2）根据各类张数可知长方形面积：（a+b）（a+2b）= a2+3ab+2b2．

(3)根据完全平方公式变形可得；

（4）设5+2x=a，2x+3=b，则a2+b2=60，a﹣b=2，再运用完全平方公式可得.

解：（1）（a+b）2=a2+2ab+b2；

（2）如图，

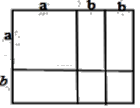
（a+b）（a+2b）=a2+3ab+2b2．

（3）∵a2+b2=57，ab=12，

∴（a+b）2=a2+b2+2ab=81，

∵a+b＞0，

∴a+b=9；

（4）设5+2x=a，2x+3=b，

则a2+b2=60，a﹣b=2，

∵（a﹣b）2=a2+b2﹣2ab

∴60﹣2ab=4，∴ab=28，

∴（5+2x）（2x+3）=28．