【题目】如图,AB 是⊙O 的直径,点C 是⊙O 上一点,AD 与过点C的切线垂直,垂足为 D,直线 DC 与AB 的延长线相交于点P,弦CE 平分∠ACB,交AB 于点F,连接BE.

求证:(1)AC 平分∠DAB;
(2)△PCF 是等腰三角形.
参考答案:
【答案】详见解析.
【解析】试题分析:
(1)由已知条件证AD∥OC可得∠DAC=∠ACO;由OA=OC可得∠ACO=∠CAO;两者结合可得∠DAC=∠CAO,从而可得AC平分∠DAB;
(2)由AD⊥DC,AB 是⊙O 的直径,可得∠ADC=∠ACB=90°,从而可得∠DAC+∠DCA=∠DCA+∠PCB=90°,这样可得∠DAC=∠PCB=∠CAO;由CE平分∠ACB可得∠ACF=∠BCF,这样可得∠CAO+∠ACF=∠PCB+∠BCF,结合三角形外角性质可证得:∠PCF=∠PFC,从而可得PC=PF,就可得△PCF是等腰三角形.
试题解析:
(1)∵ PD 切⊙O 于点C,
∴OC⊥PD,
又AD⊥PD,
∴OC∥AD,
∴∠ACO=∠DAC,
又OC=OA,
∴∠ACO=∠CAO,
∴∠DAC=∠CAO,
即AC 平分∠DAB.
(2)∵AD⊥PD,
∴∠DAC+∠ACD=90°,
又AB 为⊙O 的直径,
∴∠ACB=90°,
∴∠PCB+∠ACD=90°,
∴∠DAC=∠PCB,
又∠DAC=∠CAO,
∴∠CAO=∠PCB,
∵CE 平分∠ACB,
∴∠ACF=∠BCF,
∴∠CAO+∠ACF=∠PCB+∠BCF,
∴∠PFC=∠PCF,
∴△PCF 是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线 l1∥l2,l3 和 l1,l2 分别交于 C,D 两点,点 A,B 分别在线 l1,l2 上,且位于 l3 的左 侧,点 P 在直线 l3 上,且不和点 C,D 重合.
(1)如图 1,有一动点 P 在线段 CD 之间运动时,试确定∠1、∠2、∠3 之间的关系,并给出证明;
(2)如图 2,当动点 P 在线段 CD 之外运动时,上述的结论是否成立?若不成立,并给出证明.
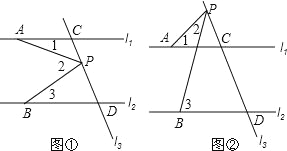
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中适合采用普查的是( ).
A.某校七年级1班学生的视力情况B.了解某市快递包裹产生包装垃圾的数量
C.检查一批灯泡的使用寿命D.对我市“今日说法”栏目收视率的调查
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,将含
 的三角尺的直角顶点
的三角尺的直角顶点 落在第二象限,其斜边两端点
落在第二象限,其斜边两端点 、
、 分别落在
分别落在 轴、
轴、 轴上,且
轴上,且 .
.(
 )若
)若 .
.①求点
 的坐标.
的坐标.②若点
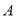 向右滑动
向右滑动 ,求点
,求点 向上滑动的距离.
向上滑动的距离.(
 )点
)点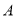 、
、 分别在
分别在 轴、
轴、 轴上滑动,则点
轴上滑动,则点 于点
于点 的距离的最大值
的距离的最大值 __________
__________  .(直接写出答案)
.(直接写出答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
 的图像与
的图像与 轴、
轴、 轴分别相交于点
轴分别相交于点 、
、 ,点
,点 在该函数的图像上,
在该函数的图像上,  到
到 轴、
轴、 轴的距离分别为
轴的距离分别为 、
、 .
.(
 )当
)当 为线段
为线段 端点
端点 时,求
时,求 的值.
的值.(
 )直接写出
)直接写出 的范围,并求当
的范围,并求当 时点
时点 的坐标.
的坐标.(
 )若在线段
)若在线段 上存在无数个
上存在无数个 点,使
点,使 (
( 为常数),求
为常数),求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( )

A. 2个 B. 3个 C. 4个 D. 无数个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的有( )
①延长直线AB ②延长线段AB ③延长射线AB
④画直线AB=5cm ⑤在射线AB上截取线段AC,使AC=5cm
A.1个B.2个C.3个D.4个
相关试题

