【题目】如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC 上,以AD为折痕△ABD折叠得到△AB′D,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是 . 
参考答案:
【答案】2或5
【解析】解:∵Rt△ABC纸片中,∠C=90°,AC=6,BC=8,
∴AB=10,
∵以AD为折痕△ABD折叠得到△AB′D,
∴BD=DB′,AB′=AB=10.
如图1所示:当∠B′DE=90°时,过点B′作B′F⊥AF,垂足为F.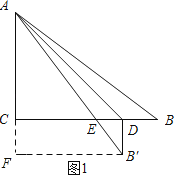
设BD=DB′=x,则AF=6+x,FB′=8﹣x.
在Rt△AFB′中,由勾股定理得:AB′2=AF2+FB′2 , 即(6+x)2+(8﹣x)2=102 .
解得:x1=2,x2=0(舍去).
∴BD=2.
如图2所示:当∠B′ED=90°时,C与点E重合.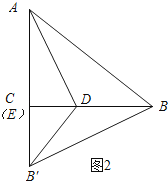
∵AB′=10,AC=6,
∴B′E=4.
设BD=DB′=x,则CD=8﹣x.
在Rt△′BDE中,DB′2=DE2+B′E2 , 即x2=(8﹣x)2+42 .
解得:x=5.
∴BD=5.
综上所述,BD的长为2或5.
所以答案是:2或5.
【考点精析】根据题目的已知条件,利用翻折变换(折叠问题)的相关知识可以得到问题的答案,需要掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
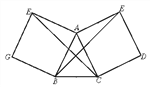
查看答案和解析>>【题目】如图4,四边形ACDE、BAFG是以△ABC的边AC、AB为边向△ABC外所作的正方形.
求证:(1)EB=FC.(2)EB⊥FC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店在2014年至2016年期间销售一种礼盒.2014年,该商店用3500元购进了这种礼盒并且全部售完;2016年,这种礼盒的进价比2014年下降了11元/盒,该商店用2400元购进了与2014年相同数量的礼盒也全部售完,礼盒的售价均为60元/盒.
(1)2014年这种礼盒的进价是多少元/盒?
(2)若该商店每年销售这种礼盒所获利润的年增长率相同,问年增长率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足.设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A在数轴上,从点A出发,沿数轴向右移动3个单位长度到达点C,点B所表示的有理数是5的相反数,按要求完成下列各小题.
(1)请在数轴上标出点B和点C;
(2)求点B所表示的有理数与点C所表示的有理数的乘积;
(3)若将该数轴进行折叠,使得点A和点B重合,则点C和数 所表示的点重合.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B两点在数轴上对应的数分别为a,b,且点A在点B的左边,|a|=10,a+b=80,ab<0.
(1)求出a,b的值;
(2)现有一只电子蚂蚁P从点A出发,以3个单位长度/秒的速度向右运动,同时另一只电子蚂蚁Q从点B出发,以2个单位长度/秒的速度向左运动.
①设两只电子蚂蚁在数轴上的点C相遇,求出点C对应的数是多少?
②经过多长时间两只电子蚂蚁在数轴上相距20个单位长度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】由6根钢管首尾顺次铰接而成六边形钢架ABCDEF,相邻两钢管可以转动.已知各钢管的长度为AB=DE=1米,BC=CD=EF=FA=2米.(铰接点长度忽略不计)

(1)转动钢管得到三角形钢架,如图1,则点A,E之间的距离是米.
(2)转动钢管得到如图2所示的六边形钢架,有∠A=∠B=∠C=∠D=120°,现用三根钢条连接顶点使该钢架不能活动,则所用三根钢条总长度的最小值是米.
相关试题

