【题目】 如图,已知△ABC,AB=AC=1,∠A=36°,∠ABC的平分线BD交AC于点D,则AD的长是 , cosA的值是 . (结果保留根号) 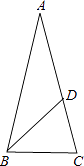
参考答案:
【答案】![]() ;
;![]()
【解析】解:∵△ABC,AB=AC=1,∠A=36°, ∴∠ABC=∠ACB= ![]() =72°.
=72°.
∵BD是∠ABC的平分线,
∴∠ABD=∠DBC= ![]() ∠ABC=36°.
∠ABC=36°.
∴∠A=∠DBC=36°,
又∵∠C=∠C
∴△ABC∽△BDC,
∴ ![]() ,
,
设AD=x,则BD=BC=x.则 ![]() =
= ![]() ,
,
解得:x= ![]() (舍去)或
(舍去)或 ![]() .
.
故x= ![]() .
.
如右图,过点D作DE⊥AB于点E,
∵AD=BD,
∴E为AB中点,即AE= ![]() AB=
AB= ![]() .
.
在Rt△AED中,cosA=  =
= ![]() .
.
故答案是: ![]() ;
; ![]() .
.
【考点精析】掌握黄金分割和相似三角形的判定与性质是解答本题的根本,需要知道把线段AB分成两条线段AC,BC(AC>BC),并且使AC是AB和BC的比例中项,叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点,其中AC=0.618AB;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+2
 =(1+
=(1+ )2.善于思考的小明进行了以下探索:设a+b
)2.善于思考的小明进行了以下探索:设a+b =(m+n
=(m+n )2(其中a,b,m,n均为整数),则有a+b
)2(其中a,b,m,n均为整数),则有a+b =m2+2n2+2mn
=m2+2n2+2mn ,∴a=m2+2n2,b=2mn.这样小明就找到了一种把类似a+b
,∴a=m2+2n2,b=2mn.这样小明就找到了一种把类似a+b 的式子化为平方式的方法.请你仿照小明的方法解决下列问题:
的式子化为平方式的方法.请你仿照小明的方法解决下列问题:(1)当a,b,m,n均为正整数时,若a+b
 =(m+n
=(m+n )2,用含m,n的式子分别表示a,b,得a=______________,b=________;
)2,用含m,n的式子分别表示a,b,得a=______________,b=________;(2)利用所探索的结论,找一组正整数a,b,m,n填空:
________+________
 =(________+________
=(________+________ )2;
)2;(3)若a+4
 =(m+n
=(m+n )2,且a,m,n均为正整数,求a的值.
)2,且a,m,n均为正整数,求a的值.(4)试化简
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=﹣x+6于A、B两点,若反比例函数y=
 (x>0)的图象与△ABC有公共点,则k的取值范围是( )
(x>0)的图象与△ABC有公共点,则k的取值范围是( )
A.2≤k≤9
B.2≤k≤8
C.2≤k≤5
D.5≤k≤8 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从热气球C处测得地面A、B两点的俯角分别是30°、45°,如果此时热气球C处的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )

A.200米
B.200 米
米
C.220 米
米
D.100( +1)米
+1)米 -
科目: 来源: 题型:
查看答案和解析>>【题目】“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
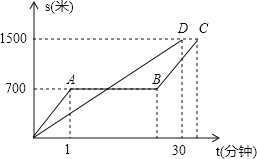
(1)填空:折线OABC表示赛跑过程中 的路程与时间的关系,线段OD表示赛跑过程中 的路程与时间的关系.赛跑的全程是 米.
(2)兔子在起初每分钟跑 米,乌龟每分钟爬 米.
(3)乌龟用了 分钟追上了正在睡觉的兔子.
(4)兔子醒来,以48千米/时的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟?
-
科目: 来源: 题型:
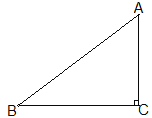
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=4cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣B﹣C﹣A运动,设运动时间为t秒(t>0).
(1)若点P在BC上,且满足PA=PB,求此时t的值;
(2)若点P恰好在∠ABC的角平分线上,求此时t的值;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.

(1)求证:四边形BDFC是平行四边形;
(2)若△BCD是等腰三角形,求四边形BDFC的面积.
相关试题

