【题目】如图,在![]() 中,已知
中,已知![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点,点
的中点,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 边上运动(点
边上运动(点![]() 不与点
不与点![]() 、
、![]() 重合),且保持
重合),且保持![]() ,连接
,连接![]() 、
、![]() 、
、![]() .在此运动变化的过程中,有下列结论,其中正确的结论是( )
.在此运动变化的过程中,有下列结论,其中正确的结论是( )
①四边形![]() 有可能成为正方形;②
有可能成为正方形;②![]() 是等腰直角三角形;
是等腰直角三角形;
③四边形![]() 的面积是定值;④点
的面积是定值;④点![]() 到线段
到线段![]() 的最大距离为
的最大距离为![]() .
.
A. ①④ B. ①②③ C. ①②④ D. ①②③④
参考答案:
【答案】D
【解析】①当DE⊥AC,DF⊥BC时,此时四边形CEDF是矩形,由AC=BC,∠ACB=90°,则∠A=∠B=45°,由CD⊥AB,则∠ACD=∠BCD=45°,则AD=CD=BD,同理CE=AE=DE,则此时四边形CEDF是正方形,正确;
②连接CD,在△ADE和△CDF中,AE=CF, ∠A=∠DCF=45°,AD=CD,
∴△ADE≌△CDF,
∴ED=DF,∠CDF=∠EDA,
又∵∠ADE+∠EDC=90°,
∴∠EDC+∠CDF=90°=∠EDF,
∴△DFE为等腰直角三角形,正确;
③∵△ADE≌△CDF,
∴S△ADE=S△CDF,
∵S四边形CEDF=S△CED+S△CFD,
∴S四边形CEDF=S△CED+S△AED=S△ADC,
∵S△ADC=![]() S△ABC=4,
S△ABC=4,
∴四边形CEDF面积是定值为4,正确;
④设C到EF的距离为d,CF=x,
∵△DEF是等腰直角三角形,故D到EF的距离为![]() EF,
EF,
又四边形CEDF的面积是定值4,
故S四边形CEDF=S△CEF+S△FED=![]() (
(![]() +d)=4,
+d)=4,
则d=![]()
![]() ,当EF越小,则d越大,
,当EF越小,则d越大,
由EF=![]() DE,则DE最小时,EF最小,此时d最大.
DE,则DE最小时,EF最小,此时d最大.
而当DE⊥AC时,DE=2最小,
此时EF=2![]() ,d=
,d=![]()
![]() =
=![]() .
.
故正确.
综上,①②③④都正确.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:∠C=∠D,OD=OC.求证:DE=CE.

【答案】证明见解析
【解析】试题分析:利用ASA证明△OBC≌△OAD,根据全等三角形的对应边相等可得OA=OB,再由OD=OC,即可得AC=BD,根据AAS证明△ACE≌△BDE,再由全等三角形的对应边相等即可得结论.
试题解析:
在△OBC和△OAD中,
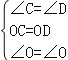 ,
,∴△OBC≌△OAD(ASA),
∴OA=OB,
∵OD=OC,
∴OD﹣OB=OC﹣OA,即AC=BD,
在△ACE和△BDE中,
 ,
,∴△ACE≌△BDE(AAS),
∴DE=CE.
【题型】解答题
【结束】
27【题目】如图,以等腰直角三角形ABC的斜边AB为边向内作等边△ABD,连接DC,以DC为边,作等边△DCE,点B、E在CD的同侧.
(1)求∠BCE的大小;
(2)求证:BE=AC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】2012年,义乌市城市居民人均可支配收入约为44500元,居全省县级市之首,数字44500用科学记数法可表示为( )
A.4.45×103
B.4.45×104
C.4.45×105
D.4.45×106 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣2)5÷(﹣2)3的结果是( )
A. ﹣4B. 4C. ﹣2D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中的每个小正方形边长都是
 ,图中虚线叫做格线,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形(只要求画出图形,不写作法和结
,图中虚线叫做格线,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形(只要求画出图形,不写作法和结论,作图需用黑笔描画):
(
 )使三角形为直角三角形,且不以格线为任意一边(在图
)使三角形为直角三角形,且不以格线为任意一边(在图 中画一个即可);
中画一个即可);(
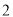 )使三角形的三边长分别为
)使三角形的三边长分别为 ,
, 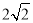 ,
,  (在图
(在图 中画一个即可);
中画一个即可);(
 )使三角形为钝角三角形且面积为
)使三角形为钝角三角形且面积为 (在图
(在图 中画一个即可).
中画一个即可).


-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某商品的进价为每件30元,九(1)班数学兴趣小组经过市场调查,整理出该商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
第x天
1≤x<50
50≤x≤90
售价(元/件)
x+40
90
每天销量(件)
200-2x
(1)分别求出第25天和第60天商家在销售该商品时所获得的利润;
(2)问销售该商品第几天时,当天的销售利润为6050元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,⊙O是△ABC的外接圆,
 =
= ,点D在边BC上,AE∥BC,AE=BD.
,点D在边BC上,AE∥BC,AE=BD.(1)求证:AD=CE;
(2)如果点G在线段DC上(不与点D重合),且AG=AD,求证:四边形AGCE是平行四边形.

相关试题

