【题目】如图,已知:∠C=∠D,OD=OC.求证:DE=CE.

【答案】证明见解析
【解析】试题分析:利用ASA证明△OBC≌△OAD,根据全等三角形的对应边相等可得OA=OB,再由OD=OC,即可得AC=BD,根据AAS证明△ACE≌△BDE,再由全等三角形的对应边相等即可得结论.
试题解析:
在△OBC和△OAD中,
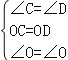 ,
,
∴△OBC≌△OAD(ASA),
∴OA=OB,
∵OD=OC,
∴OD﹣OB=OC﹣OA,即AC=BD,
在△ACE和△BDE中,
 ,
,
∴△ACE≌△BDE(AAS),
∴DE=CE.
【题型】解答题
【结束】
27
【题目】如图,以等腰直角三角形ABC的斜边AB为边向内作等边△ABD,连接DC,以DC为边,作等边△DCE,点B、E在CD的同侧.
(1)求∠BCE的大小;
(2)求证:BE=AC.

参考答案:
【答案】(1)75°(2)证明见解析
【解析】试题分析:(1)根据已知条件易证△ADC≌△BDE,根据全等三角形的性质可得BE=AC=BC,∠EBD=∠CAD=15°,根据等腰三角形的性质和三角形的内角和定理即可求得∠BCE的大小;(2)由(1)中的△ADC≌△BDE,根据全等三角形的对应边相等即可得结论.
试题解析:
(1)∵△ACB是等腰直角三角形,
∴AC=BC,∠CAB=∠CBA=45°
∵△ABD和△DEC是等边三角形,
∴AD=BD,CD=DE,∠ADB=∠EDC=60°,∠DAB=∠DBA=60°
∴∠DAC=60°﹣45°=15°,∠DBC=15°,∠EDB=∠CDA=60°﹣∠BCD,
在△ADC和△BDE中
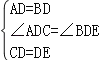
∴△ADC≌△BDE,
∴BE=AC=BC,∠EBD=∠CAD=15°,
∴∠BCE=∠BEC=![]() (180°﹣15°﹣15°)=75°;
(180°﹣15°﹣15°)=75°;
(2)证明:∵△ADC≌△BDE,
∴BE=AC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2012年末统计,杭州市常住人口是880.2万人,用科学记数法表示为人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在2,﹣2,8,6这四个数中,互为相反数的是( )
A.﹣2与2
B.2与8
C.﹣2与6
D.6与8 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(m+3,2m+4)在x轴上,那么点P的坐标为( )
A. (-1,0)B. (1,0)C. (-2,0)D. (0,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】2012年,义乌市城市居民人均可支配收入约为44500元,居全省县级市之首,数字44500用科学记数法可表示为( )
A.4.45×103
B.4.45×104
C.4.45×105
D.4.45×106 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣2)5÷(﹣2)3的结果是( )
A. ﹣4B. 4C. ﹣2D. 2
-
科目: 来源: 题型:
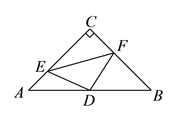
查看答案和解析>>【题目】如图,在
 中,已知
中,已知 ,
,  ,
,  是
是 的中点,点
的中点,点 、
、 分别在
分别在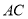 、
、 边上运动(点
边上运动(点 不与点
不与点 、
、 重合),且保持
重合),且保持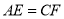 ,连接
,连接 、
、 、
、 .在此运动变化的过程中,有下列结论,其中正确的结论是( )
.在此运动变化的过程中,有下列结论,其中正确的结论是( )①四边形
 有可能成为正方形;②
有可能成为正方形;② 是等腰直角三角形;
是等腰直角三角形;③四边形
 的面积是定值;④点
的面积是定值;④点 到线段
到线段 的最大距离为
的最大距离为 .
.
A. ①④ B. ①②③ C. ①②④ D. ①②③④
相关试题

