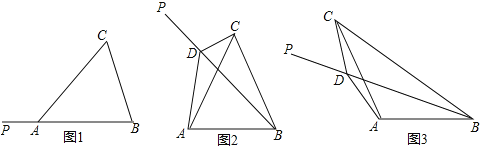
【题目】如图1,在△ABC中,AB=AC,射线BP从BA所在位置开始绕点B顺时针旋转,旋转角为α(0°<α<180°)
(1)当∠BAC=60°时,将BP旋转到图2位置,点D在射线BP上.若∠CDP=120°,则∠ACD ∠ABD(填“>”、“=”、“<”),线段BD、CD与AD之间的数量关系是 ;
(2)当∠BAC=120°时,将BP旋转到图3位置,点D在射线BP上,若∠CDP=60°,求证:BD﹣CD=![]() AD;
AD;
(3)将图3中的BP继续旋转,当30°<α<180°时,点D是直线BP上一点(点P不在线段BD上),若∠CDP=120°,请直接写出线段BD、CD与AD之间的数量关系(不必证明).
参考答案:
【答案】(1)=,BD=CD+AD;(2)证明见试题解析;(3)BD+CD=![]() AD.
AD.
【解析】
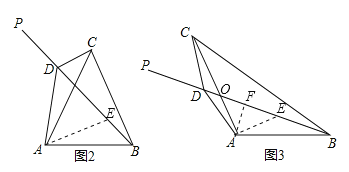
试题分析:(1)如图2,由∠CDP=120°,得出∠CDB=60°,则∠CDB=∠BAC=60°,所以A、B、C、D四点共圆,由圆周角定理得出∠ACD=∠ABD;在BP上截取BE=CD,连接AE.利用SAS证明△DCA≌△EBA,得到AD=AE,∠DAC=∠EAB,再证明△ADE是等边三角形,得到DE=AD,进而得出BD=CD+AD.
(2)如图3,设AC与BD相交于点O,在BP上截取BE=CD,连接AE,过A作AF⊥BD于F.先证△DOC∽△AOB,得到∠DCA=∠EBA.再利用SAS证明△DCA≌△EBA,得到AD=AE,∠DAC=∠EAB.由∠CAB=∠CAE+∠EAB=120°,得出∠DAE=120°,由等腰三角形的性质及三角形内角和定理求出∠ADE=∠AED=30°.解Rt△ADF,得出DF=![]() AD,那么DE=2DF=
AD,那么DE=2DF=![]() AD,进而得出BD=DE+BE=
AD,进而得出BD=DE+BE=![]() AD+CD,即BD﹣CD=
AD+CD,即BD﹣CD=![]() AD;
AD;
(3)同(2)证明可以得出BD+CD=![]() AD.
AD.
试题解析:(1)如图2,∵∠CDP=120°,∴∠CDB=60°,∵∠BAC=60°,∴∠CDB=∠BAC=60°,∴A、B、C、D四点共圆,∴∠ACD=∠ABD.在BP上截取BE=CD,连接AE.在△DCA与△EBA中,∵AC=AB,∠ACD=∠ABE,CD=BE,∴△DCA≌△EBA(SAS),∴AD=AE,∠DAC=∠EAB,∵∠CAB=∠CAE+∠EAB=60°,∴∠DAE=60°,∴△ADE是等边三角形,∴DE=AD.∵BD=BE+DE,∴BD=CD+AD.故答案为:=,BD=CD+AD;
(2)如图3,设AC与BD相交于点O,在BP上截取BE=CD,连接AE,过A作AF⊥BD于F.
∵∠CDP=60°,∴∠CDB=120°.∵∠CAB=120°,∴∠CDB=∠CAB,∵∠DOC=∠AOB,∴△DOC∽△AOB,∴∠DCA=∠EBA.在△DCA与△EBA中,∵AC=AB,∠ACD=∠ABE,CD=BE,∴△DCA≌△EBA(SAS),∴AD=AE,∠DAC=∠EAB.∵∠CAB=∠CAE+∠EAB=120°,∴∠DAE=120°,∴∠ADE=∠AED=(180°-120°)÷2=30°.∵在Rt△ADF中,∠ADF=30°,∴DF=![]() AD,∴DE=2DF=
AD,∴DE=2DF=![]() AD,∴BD=DE+BE=
AD,∴BD=DE+BE=![]() AD+CD,∴BD﹣CD=
AD+CD,∴BD﹣CD=![]() AD;
AD;
(3)BD+CD=![]() AD.
AD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=3x﹣1的图象向上平移7个单位后的解析式是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知2x+y=1,代数式(y+1)2-(y2-4x)的值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面内有三条直线,如果要使其中两条且只有两条直线平行,那么它们( )
A. 没有交点 B. 只有一个交点
C. 有两个交点 D. 有三个交点
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在线段AB上,AC=6cm,MB=10cm,点M、N分别为AC、BC的中点.
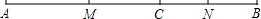
(1)求线段BC的长;
(2)求线段MN的长;
(3)若C在线段AB延长线上,且满足AC﹣BC=b cm,M,N分别是线段AC,BC的中点,你能猜想MN的长度吗?请写出你的结论(不需要说明理由). -
科目: 来源: 题型:
查看答案和解析>>【题目】在兰州市开展的“体育、艺术2+1”活动中,某校根据实际情况,决定主要开设A:乒乓球,B:篮球,C:跑步,D:跳绳这四种运动项目.为了解学生喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如下的条形统计图和扇形统计图.请你结合图中信息解答下列问题:

(1)样本中喜欢B项目的人数百分比是;
(2)把条形统计图补充完整;
(3)已知该校有1 000人,根据样本估计全校喜欢乒乓球的人数是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.哥哥的身高比弟弟高是必然事件
B.今年中秋节有雨是不确定事件
C.随机抛一枚均匀的硬币两次,都是正面朝上是不可能事件
D.“彩票中奖的概率为 ”表示买5张彩票肯定会中奖
”表示买5张彩票肯定会中奖
相关试题

