【题目】如图所示,点O为直线BD上的一点,OC⊥OA,垂足为点O,∠COD=2∠BOC,求∠AOB的度数.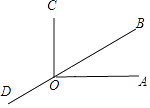
参考答案:
【答案】解:∵点O为直线BD上一点,
∴∠COD+∠B0C=180°,
将∠COD=2∠B0C代入,
得2∠BOC+∠BOC=180°,
解得∠BOC=60°,
∴∠AOB=∠COA﹣∠BOC=90°﹣60°=30°
【解析】先由点O为直线BD上一点,根据邻补角定义得出∠COD+∠BOC=180°,将∠COD=2∠B0C代入,求出∠BOC=60°,再根据∠AOB=∠COA-∠BOC即可求解.
【考点精析】通过灵活运用角的运算和垂线的性质,掌握角之间可以进行加减运算;一个角可以用其他角的和或差来表示;垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短即可以解答此题.
-
科目: 来源: 题型:
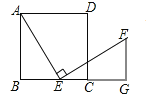
查看答案和解析>>【题目】如图,在正方形ABCD中,点E(与点B、C不重合)是BC边上一点,将线段EA绕点E顺时针旋转90°到EF,过点F作BC的垂线交BC的延长线于点G,连接CF.
(1)求证:△ABE≌△EGF;
(2)若AB=2,S△ABE=2S△ECF,求BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市用3000元购进某种干果销售,由于销售状况良好,超市又调拨9000元资金购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果数量是第一次的2倍还多300千克,如果超市按每千克9元的价格出售,当大部分干果售出后,余下的600千克按售价的8折售完.
(1)该种干果的第一次进价是每千克多少元?
(2)超市销售这种干果共盈利多少元? -
科目: 来源: 题型:
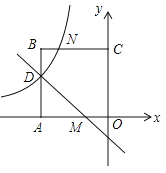
查看答案和解析>>【题目】如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点D、M分别在边AB、OA上,且AD=2DB,AM=2MO,一次函数y=kx+b的图象过点D和M,反比例函数
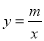 的图象经过点D,与BC的交点为N.
的图象经过点D,与BC的交点为N.(1)求反比例函数和一次函数的表达式;
(2)若点P在直线DM上,且使△OPM的面积与四边形OMNC的面积相等,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1:∠2:∠3=2:3:4,∠AFE=60°,∠BDE=120°,写出图中平行的直线,并说明理由.
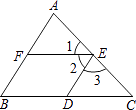
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学开展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示.
班级
平均数(分)
中位数
众数
九(1)
85
85
九(2)
80
(1)根据图示填写上表;
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)计算两班复赛成绩的方差,并说明哪个班级的成绩较稳定.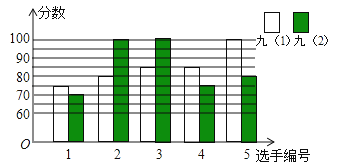
-
科目: 来源: 题型:
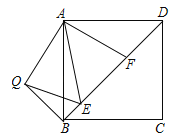
查看答案和解析>>【题目】如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证:
(1)EA是∠QED的平分线;
(2)
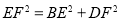 .
.
相关试题

