【题目】请阅读下面材料,并回答所提出的问题.三角形内角平分线定理:三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例.
已知:如图,△ABC中, AD是角平分线.
求证: ![]() .
.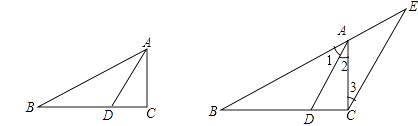
证明:过C作CE∥DA,交BA的延长线于E.
∴ ![]() . ①
. ①![]() AD是角平分线,
AD是角平分线,
∴ ![]() .
.![]()
![]() .
.![]() . ②
. ②
又 ![]() ,
,![]() . ③
. ③![]()
![]() .
.
(1)上述证明过程中,步骤①②③处的理由是什么?(写出两条即可)
(2)用三角形内角平分线定理解答:已知,△ABC中,AD是角平分线,AB=7cm,AC=4cm,BC=6cm,求BD的长;
(3)我们知道如果两个三角形的高相等,那么它们面积的比就等于底的比.请你通过研究△ABD和△ACD面积的比来证明三角形内角平分线定理.
参考答案:
【答案】
(1)解:证明过程中用到的定理有:
①平行线的性质定理;
②等腰三角形的判定定理;
③平行线分线段成比例定理
(2)解:∵AD是角平分线,
∴ ![]() ,
,
又∵AB=7cm,AC=4cm,BC=6cm,
∴ ![]() ,
,
∴BD= ![]() (cm)
(cm)
(3)解:∵△ABD和△ACD的高相等,
可得:△ABD和△ACD面积的比= 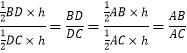 ,
,
可得: ![]()
【解析】(1)利用“平行线的性质定理;等腰三角形的判定定理;平行线分线段成比例定理”可填出答案;(2)学会应用(1)的结论,构造比例式求线段;(3)利用面积法,再结合角平分线性质定理可构造两个比例式,证得结论.
【考点精析】利用三角形的面积和角平分线的性质定理对题目进行判断即可得到答案,需要熟知三角形的面积=1/2×底×高;定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)动手操作:
如图1所示,已知A、B、C三个点都在网格纸的格点上,∠1是∠ABC的余角,∠2是∠ABC的补角,CD⊥AB于点D,CE∥AB,试在图中分别画出:∠1、∠2、垂线段CD和直线CE.
(2)已知:如图2,点E在DF上,点B在AC上,∠1=∠2,∠C=∠D,试说明:AC∥DF,请将下面的解答过程补充完整:
解:∵∠1=∠2(已知)
又∵∠1=∠3
∴ = (等量代换)
∴EC∥DB
∴∠C= (两直线平行,同位角相等)
∵∠C=∠D(已知)
∴∠D=
∴AC∥DF

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(8,8),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.
(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;判断线段HG、OH、BG的数量关系,并说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.

-
科目: 来源: 题型:
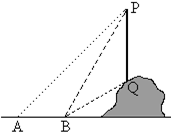
查看答案和解析>>【题目】如图所示,某数学活动小组要测量山坡上的电线杆PQ的高度.他们采取的方法是:先在地面上的点A处测得杆顶端点P的仰角是45°,再向前走到B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°,这时只需要测出AB的长度就能通过计算求出电线杆PQ的高度.你同意他们的测量方案吗?若同意,画出计算时的图形,简要写出计算的思路,不用求出具体值;若不同意,提出你的测量方案,并简要写出计算思路.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为

A.
 B.3 C.1 D.
B.3 C.1 D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:三边长和面积都是整数的三角形称为“整数三角形”.
数学学习小组的同学从32根等长的火柴棒(每根长度记为1个单位)中取出若干根,首尾依次相接组成三角形,进行探究活动.
小亮用12根火柴棒,摆成如图所示的“整数三角形”;
小颖分别用24根和30根火柴棒摆出直角“整数三角形”;
小辉受到小亮、小颖的启发,分别摆出三个不同的等腰“整数三角形”.

⑴请你画出小颖和小辉摆出的“整数三角形”的示意图;
⑵你能否也从中取出若干根,按下列要求摆出“整数三角形”,如果能,请画出示意图;如果不能,请说明理由.
①画出等边“整数三角形”;
②摆出一个非特殊(既非直角三角形,也非等腰三角形)“整数三角形”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=mx2-8mx+16m-1(m>0)与x轴的交点分别为A(x1 , 0),B(x2 , 0).
(1)求证:抛物线总与x轴有两个不同的交点;
(2)若AB=2,求此抛物线的解析式.
(3)已知x轴上两点C(2,0),D(5,0),若抛物线y=mx2-8mx+16m-1(m>0)与线段CD有交点,请写出m的取值范围.
相关试题

