【题目】(请在括号里注明重要的推理依据)
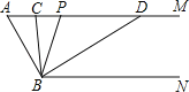
如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是 .
参考答案:
【答案】(1)∠CBD=60°;(2)不变化,∠APB=2∠ADB,证明见解析;(3)∠ABC=30°.
【解析】
试题分析:(1)由平行线的性质可求得∠ABN,再根据角平分线的定义和整体思想可求得∠CBD;
(2)由平行线的性质可得∠APB=∠PBN,∠ADB=∠DBN,再由角平分线的定义可求得结论;
(3)由平行线的性质可得到∠ACB=∠CBN=60°+∠DBN,结合条件可得到∠DBN=∠ABC,且∠ABC+∠DBN=60°,可求得∠ABC的度数.
试题解析: (1)∵AM∥BN,
∴∠A+∠ABN=180°,(两直线平行,同旁内角互补)
∵∠A=60°
∴∠ABN=120°
∵BC、BD分别平分∠ABP和∠PBN,
∴∠CBP=![]() ∠ABP, ∠DBP=
∠ABP, ∠DBP=![]() ∠NBP,
∠NBP,
∴∠CBD=![]() ∠ABN=60°
∠ABN=60°
(2)不变化,∠APB=2∠ADB
证明∴ ∵AM∥BN,
∴∠APB=∠PBN (两直线平行,内错角相等)
∠ADB=∠DBN (两直线平行,内错角相等)
又∵BD平分∠PBN,
∴∠PBN =2∠DBN
∴∠APB=2∠ADB
(3)∠ABC=30°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正n边形的一个外角是45°,则n=____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一架云梯AB长25米,如图那样斜靠在一面墙AC上,这时云梯底端B离墙底C的距离BC为7米.
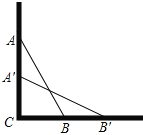
(1)这云梯的顶端距地面AC有多高?
(2)如果云梯的顶端A下滑了4米,那么它的底部B在水平方向向右滑动了多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各式及其展开式:
 ;
;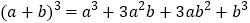 ;
;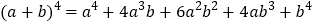 ;
;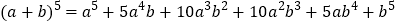 ;…
;…请你猜想
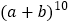 的展开式第三项的系数是( )
的展开式第三项的系数是( )A. 36 B. 45 C. 55 D. 66
-
科目: 来源: 题型:
查看答案和解析>>【题目】求代数式5(2a2b ab2) 3(ab2 + 3a2b)的值,其中a = 2,b = 1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个多边形的一个内角和等于1440°,那么从这个多边形的一个顶点出发有___条对角线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(5,6)关于y轴对称的点是( )
A. (6,5) B. (-5,6) C. (5,-6) D. (-5,-6)
相关试题

