【题目】如图,∠AOB=30°,OP平分∠AOB,PC⊥OB于点C.若OC=2,则PC的长是 . 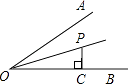
参考答案:
【答案】4﹣2 ![]()
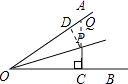
【解析】解:延长CP,与OA交于点Q,过P作PD⊥OA, ∵OP平分∠AOB,PD⊥OA,PC⊥OB,
∴PD=PC,
在Rt△QOC中,∠AOB=30°,OC=2,
∴QC=OCtan30°=2× ![]() =
= ![]() ,∠APD=30°,
,∠APD=30°,
在Rt△QPD中,cos30°= ![]() =
= ![]() ,即PQ=
,即PQ= ![]() DP=
DP= ![]() PC,
PC,
∴QC=PQ+PC,即 ![]() PC+PC=
PC+PC= ![]() ,
,
解得:PC=4﹣2 ![]() .
.
所以答案是:4﹣2 ![]() .
.
【考点精析】本题主要考查了含30度角的直角三角形和勾股定理的概念的相关知识点,需要掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题:①对顶角相等;②同位角相等,两直线平行;③若|a|=|b|,则a=b;④若x=2,则2|x|-1=3.以上命题是真命题的有( ).
A. ①②③④ B. ①④ C. ②④ D. ①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程m(x+h)2+k=0(m,h,k均为常数,m≠0)的解是x1=﹣3,x2=2,则方程m(x+h﹣3)2+k=0的解是( )
A.x1=﹣6,x2=﹣1
B.x1=0,x2=5
C.x1=﹣3,x2=5
D.x1=﹣6,x2=2 -
科目: 来源: 题型:
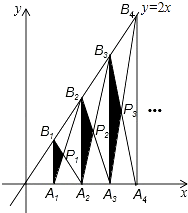
查看答案和解析>>【题目】如图,已知A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1 , 连接A1B2、B1A2、A2B3、B2A3、…、AnBn+1、BnAn+1 , 依次相交于点P1、P2、P3、…、Pn . △A1B1P1、△A2B2P2、△AnBnPn的面积依次记为S1、S2、S3、…、Sn , 则Sn为( )
A.
B.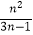
C.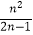
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD,EF相交于点O.
(1)写出∠COE的邻补角;
(2)分别写出∠COE和∠BOE的对顶角;
(3)如果∠BOD=60°,∠BOF=90°,求∠AOF和∠FOC的度数.

-
科目: 来源: 题型:
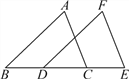
查看答案和解析>>【题目】如图,△ABC沿直线l向右移了3厘米,得△FDE,且BC=6厘米,∠B=40°.
(1)求BE;
(2)求∠FDB的度数;
(3)找出图中相等的线段(不另添加线段);
(4)找出图中互相平行的线段(不另添加线段).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CB∥OA,∠B=∠A=100°,E、F在CB上,且满足∠FOC=∠AOC,OE平分∠BOF.
(1)求∠EOC的度数;
(2)若平行移动AC,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值;
(3)在平行移动AC的过程中,是否存在某种情况,使∠OEB=∠OCA?若存在,求出∠OCA度数;若不存在,说明理由.

相关试题

