【题目】某超市准备购进甲、乙两种品牌的文具盒,甲、乙两种玩具盒的进价和售价如下表,预计购进乙品牌文具盒的数量y(个)与甲品牌玩具盒数量x(个)之间的函数关系如图所示.
甲 | 乙 | |
进价(元) | 15 | 30 |
售价(元) | 20 | 38 |
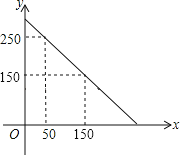
(1)y与x之间的函数关系式是 ;
(2)若超市准备用不超过6000元购进甲、乙两种文具盒,则至少购进多少个甲种文具盒?
(3)在(2)的条件下,写出销售所得的利润W(元)与x(个)之间的关系式,并求出获得的最大利润.
参考答案:
【答案】(1) y=-x+300;(2) 至少购进多200甲种文具盒;(3)W=-3x+2400,最大利润1800元
【解析】
(1)利用待定系数法即可解决问题;
(2)构建不等式即可解决问题;
(3)根据一次函数,利用一次函数的性质即可解决问题;
(1)设y=kx+b,把(50,250),(150,150)代入得:
![]() ,
,
解得![]() ,
,
∴y=-x+300.
故答案是:y=-x+300.
(2)由题意:15x+30(-x+300)≤6000,
解得x≥200,
∴至少购进多200甲种文具盒.
(3)w=5x+8(-x+300)=-3x+2400,
∵y随x的增大而减少,x≥200,
∴x=200时,y有最大值,最大值=1800(元).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB=8(点A在点B的左侧)
(1)若在直线AB上取一点C,使得AC=3CB,点D是CB的中点,求AD的长;
(2)若M是线段AB的中点,点P是线段AB延长线上任意一点,请说明PA+PB﹣2PM是一个定值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某快递公司针对新客户优惠收费,首件物品的收费标准为:若重量不超过10千克,则免运费;当重量为
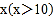 千克时,运费为
千克时,运费为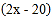 元;第二件物品的收费标准为:当重量为
元;第二件物品的收费标准为:当重量为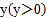 千克时,运费为
千克时,运费为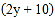 元。
元。(1)若新客户所奇首件物品的重量为13千克,则运费是多少元?
(2)若新客户所寄首件物品的运费为32元,则物品的重量是多少千克?
(3)若新客户所寄首件物品与第二件物品的重量之比为2:5,共付运费为60元,则两件物品的重量各是多少千克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义[x]表示不超过实数x的最大整数,如[1.8]=1,[﹣1.4]=﹣2,[﹣3]=﹣3.函数y=[x]的图象如图所示,则方程[x]=
 x2的解为( )#N.
x2的解为( )#N.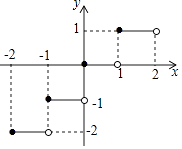
A.0或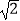
B.0或2
C.1或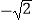
D.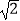
或﹣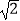
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E.若△CDE的周长为10,则AB+AD的值是( )
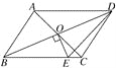
A. 10
B. 15
C. 25
D. 30
-
科目: 来源: 题型:
查看答案和解析>>【题目】东东玩具商店用500元购进一批悠悠球,很受中小学生欢迎,悠悠球很快售完,接着又用900元购进第二批这种悠悠球,所购数量是第一批数量的1.5倍,但每套进价多了5元.
(1)求第一批悠悠球每套的进价是多少元;
(2)如果这两批悠悠球每套售价相同,且全部售完后总利润不低于25%,那么每套悠悠球的售价至少是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,猜想线段DE、AD与BE有怎样的数量关系?请写出这个关系(不用证明)
(2)当直线MN绕点C旋转到图2的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
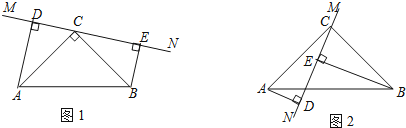
相关试题

