【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点
轴分别相交于点![]() 和点
和点![]() .
.
(1)直接写出坐标:点![]() ,点
,点![]() .
.
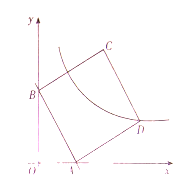
(2)以线段![]() 为一边在第一象限内作正方形
为一边在第一象限内作正方形![]() .
.
则:①顶点![]() 的坐标是 ,
的坐标是 ,
②若点![]() 在双曲线
在双曲线![]() 上,试探索:将正方形
上,试探索:将正方形![]() 沿
沿![]() 轴向左平移多少个单位长度时,点
轴向左平移多少个单位长度时,点![]() 恰好落在该双曲线上.
恰好落在该双曲线上.
参考答案:
【答案】(1)![]() ;(2)①
;(2)①![]() ;②将正方形
;②将正方形![]() 沿
沿![]() 轴向左平移1个单位长度时,点
轴向左平移1个单位长度时,点![]() 恰好落在该双曲线上
恰好落在该双曲线上
【解析】
(1)利用一次函数图象上点的坐标特征可求出点A,B的坐标;
(2)①过点D作DE⊥x轴于点E,易证△OAB≌△EDA,利用全等三角形的性质可求出点D的坐标;
②由点D的坐标,利用待定系数法可求出双曲线的解析式,过点C作CF⊥y轴于点F,易证△CFB≌△AOB,利用全等三角形的性质可求出点C的坐标,再利用反比例函数图象上点的坐标特征可得出当点C落在双曲线上时正方形ABCD沿x轴向左平移的距离.
当x=0时,y=-2x+2=2,
∴点B的坐标为(0,2);
当y=0时,-2x+2=0,
解得:x=1,
∴点A的坐标为(1,0).
故答案为:(1,0);(0,2).
(2)①过点D作DE⊥x轴于点E,如图1所示.
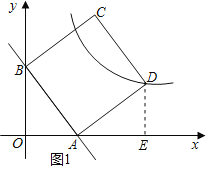
∵∠OBA+∠OAB=90°,∠OAB+∠EAD=90°,
∴∠OBA=∠EAD.
在△OAB和△EDA中,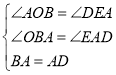 ,
,
∴△OAB≌△EDA(AAS),
∴AE=BO=2,DE=AO=1,
∴点D的坐标为(3,1).
②将点D(3,1)代入y=![]() ,得:1=
,得:1=![]() ,
,
∴k=3,
∴y=![]()
过点C作CF⊥y轴于点F,如图2所示.
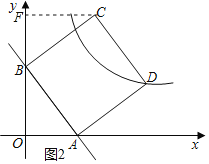
同(1)可证出△CFB≌△AOB,
∴BF=AO=1,CF=BO=2,
∴点C的坐标为(2,3).
当y=3时,![]() =3,
=3,
解得:x=1,
∵2-1=1,
∴将正方形ABCD沿x轴向左平移1个单位长度时,点C恰好落在该双曲线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板中的两块直角三角尺的直角顶点
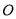 按如图方式叠放在一起.
按如图方式叠放在一起.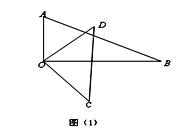
(1)如图(1)若
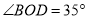 ,求
,求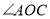 的度数,若
的度数,若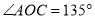 ,求
,求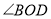 的度数;
的度数;(2)如图(2)若
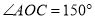 ,求
,求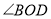 的度数;
的度数;(3)猜想
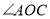 与
与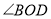 的数量关系,并结合图(1)说明理由;
的数量关系,并结合图(1)说明理由;(4)三角尺
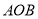 不动,将三角尺
不动,将三角尺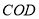 的
的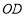 边与
边与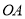 边重合,然后绕点
边重合,然后绕点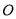 按顺时针或逆时针方向任意转动一个角度,当
按顺时针或逆时针方向任意转动一个角度,当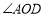 (
(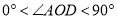 )等于多少度时,这两块三角尺各有一条边互相垂直,直接写出
)等于多少度时,这两块三角尺各有一条边互相垂直,直接写出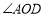 角度所有可能的值,不用说明理由.
角度所有可能的值,不用说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学对全校1200名学生进行“校园安全知识”的教育活动,从1200名学生中随机抽取部分学生进行测试,成绩评定按从高分到低分排列分为
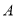 ,
,  ,
, 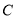 ,
,  四个等级,绘制了图①、图②两幅不完整的统计图.请结合图中所给信息解答下列问题:
四个等级,绘制了图①、图②两幅不完整的统计图.请结合图中所给信息解答下列问题: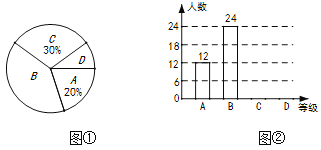
(1)求本次被抽查的学生共有多少名?
(2)将条形统计图和扇形统计图补充完整;
(3)求扇形统计图中“
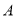 ”所在的扇形圆心角的度数;
”所在的扇形圆心角的度数;(4)估计全校“
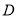 ”等级的学生有多少名?
”等级的学生有多少名? -
科目: 来源: 题型:
查看答案和解析>>【题目】近几年,随着电子商务的快速发展,“电商包裹件”占“快递件”总量的比例逐年增长,根据企业财报,某网站得到如下统计表:
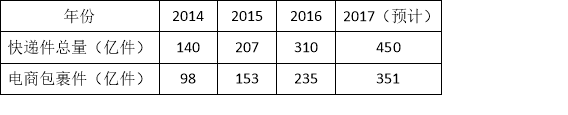
(1)请选择适当的统计图,描述2014﹣2017年“电商包裹件”占当年“快递件”总量的百分比(精确到1%);
(2)若2018年“快递件”总量将达到675亿件,请估计其中“电商包裹件”约为多少亿件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“绿水青山就是金山银山”,市民积极参与义务植树活动,小刚同学为了了解自己小区300户家庭在2019年3月义务植树的数量,进行了抽样调查,随机抽取了其中30户家庭,收集的数据如下:(单位:颗)
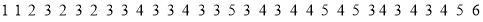
(1)对以上数据进行整理、描述和分析
①绘制如下的统计图,请补充完整
②这30户家庭2019年3月份义务植树数量得中位数是 ,众数是 .
(2)“互联网
 全民义务植树”是新时代首次全民义务植树组织形式和尽责方式的一大创新,并推出义务植树网上预约服务,小刚同学所调查的这30户家庭有7户家庭采用的网上预约义务植树这种方式,由此可以估计该小区采用这种形式的家庭有多少户?
全民义务植树”是新时代首次全民义务植树组织形式和尽责方式的一大创新,并推出义务植树网上预约服务,小刚同学所调查的这30户家庭有7户家庭采用的网上预约义务植树这种方式,由此可以估计该小区采用这种形式的家庭有多少户?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在不透明的袋子中有四张标着数字1,2,3,4的卡片,小明、小华两人按照各自的规则玩抽卡片游戏.
小明画出树状图如图所示:
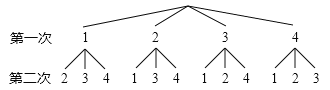
小华列出表格如下:

回答下列问题:
(1)根据小明画出的树形图分析,他的游戏规则是,随机抽出一张卡片后 (填“放回”或“不放回”),再随机抽出一张卡片;
(2)根据小华的游戏规则,表格中①表示的有序数对为 ;
(3)规定两次抽到的数字之和为奇数的获胜,你认为谁获胜的可能性大?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,∠AOC=90°,
(1)比较∠AOD,∠EOB,∠AOE的大小.
(2)若∠EOC=28°,求∠EOB和∠EOD的度数.

相关试题

