【题目】如图,在△ABC中,∠ACB=90°,BC=nAC,CD⊥AB于D,点P为AB边上一动点,PE⊥AC,PF⊥BC,垂足分别为E、F.

(1)若n=2,则![]() = ;
= ;
(2)当n=3时,连EF、DF,求![]() 的值;
的值;
(3)若![]() ,求n的值.
,求n的值.
参考答案:
【答案】(1)![]() (2)
(2)![]() (3)tanB=AC:BC的值 为
(3)tanB=AC:BC的值 为![]()
【解析】试题分析:(1)根据∠ACB=90°,PE⊥AC,PF⊥BC,那么CEPF就是个矩形.得到CE=PF从而不难求得CE:BF的值;
(2)可通过构建相似三角形来求解;
(3)可根据(2)的思路进行反向求解,即先通过EF,DF的比例关系,求出DE:DF的值.也就求出了CE:BF的值即tanB=AC:BC的值.
试题解析:
(1)∵∠ACB=90,PE⊥AC,PF⊥BC,
∴四边形CEPF是矩形.
∴CE=PF.
∴CE:BF=PF:BF=tanB=AC:BC=![]() .
.
故答案是: ![]() .
.
(2)连DE,∵∠ACB=90°,PE⊥CA,PF⊥BC,
∴四边形CEPF是矩形.
∴CE=PF.
∴CE:BF=CD:BD=PF:BF=tanB.
∵∠ACB=90°,CD⊥AB,
∴∠B+∠A=90°,∠ECD+∠A=90°,
∴∠ECD=∠B,
∴△CED∽△BFD.
∴∠EDC=∠FDB.
∵∠FDB+∠CDF=90°,
∴∠CDE+∠CDF=90°.
∴∠EDF=90°.
∵DEDF=tanB=![]() ,设DE=a,DF=3a,
,设DE=a,DF=3a,
在直角三角形EDF中,根据勾股定理可得:EF=![]() a.
a.
∴![]() .
.
(3)可根据(2)的思路进行反向求解,即先通过EF,DF的比例关系,求出DE:DF的值.也就求出了CE:BF的值,即tanB=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形两边的长分别为4和10,则此三角形的第三边长可能是( )
A.5B.6C.11D.16
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,BC边上的高AD=6,E是高AD上的一个动点,F是边AB的中点,在点E运动的过程中,存在EB+EF的最小值,则这个最小值是( )

A.3
B.4
C.5
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(﹣2,4),B(4,2),C(2,﹣1)

(1)作△ABC关于x轴的对称图形△A1B1C1 , 写出点C关于x轴的对称点C1的坐标;
(2)P为x轴上一点,请在图中画出使△PAB的周长最小时的点P并直接写出此时点P的坐标(保留作图痕迹). -
科目: 来源: 题型:
查看答案和解析>>【题目】南澳大桥是广东省第一座真正意义的跨海大桥,该桥全长约11100m,用科学记数法表示这个数为( ).
A.1.11×104mB.11.1×103 mC.0.111×104mD.1.11×103m
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x+1)(mx﹣1)(m是常数)的计算结果中,不含一次项,则m的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学校开展的“学习交通安全知识,争做文明中学生”主题活动月中,学校德工处随机选取了该校部分学生,对闯红灯情况进行了一次调查,调查结果有三种情况:A.从不闯红灯;B.偶尔闯红灯;C经常闯红灯.德工处将调查的数据进行了整理,并绘制了尚不完整的统计图如下,请根据相关信息,回答下列问题:
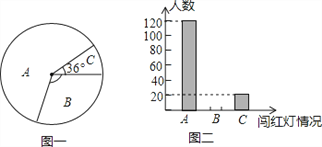
(1)本次活动共调查了_______名学生;
(2)请补全(图二),并求(图一)中 B区域的圆心角的度数_______;
(3)若该校有2400名学生,请估算该校 不严格遵守信号灯指示的有____人数.
相关试题

