【题目】如图,在等边三角形ABC中,BC边上的高AD=6,E是高AD上的一个动点,F是边AB的中点,在点E运动的过程中,存在EB+EF的最小值,则这个最小值是( )
A.3
B.4
C.5
D.6
参考答案:
【答案】D
【解析】连接CF.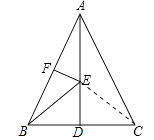
∵等边△ABC中,AD是BC边上的中线,
∴AD是BC边上的高线,即AD垂直平分BC,
∴EB=EC.当C、F、E三点共线时,EF+EC=EF+BE=CF
. ∵等边△ABC中,F是AB边的中点,
∴AD=CF=6,
∴EF+BE的最小值为6.
所以答案是:D.
【考点精析】解答此题的关键在于理解轴对称-最短路线问题的相关知识,掌握已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产的A种产品,它的成本是2元,售价是3元,年销售量为100万件,为了获得更好的效益,公司准备拿出一定的资金做广告. 根据经验,每年投入的广告费是x(10万元)时,产品的年销售量将是原销售量的y倍,且y是x的二次函数,它们的关系如下表:
x(10万元)
0
1
2
…
y
1
1.5
1.8
…
(1)求y与x的函数关系式;
(2)如果把利润看做是销售总额减去成本费和广告费,试写出年利润S(10万元)与广告费x(10万元)的函数关系式;
(3)如果投入的年广告费为10~30万元,问广告费在什么范围内,公司获得的年利润随广告费的增大而增大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的 切线,交OD的延长线于点E,连接BE、AD并延长AD交BE于点F,

(1)求证:BE是⊙O的切线
(2)若OB=9,sin∠ABC=
 ,求BF的长
,求BF的长 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形两边的长分别为4和10,则此三角形的第三边长可能是( )
A.5B.6C.11D.16
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(﹣2,4),B(4,2),C(2,﹣1)

(1)作△ABC关于x轴的对称图形△A1B1C1 , 写出点C关于x轴的对称点C1的坐标;
(2)P为x轴上一点,请在图中画出使△PAB的周长最小时的点P并直接写出此时点P的坐标(保留作图痕迹). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,BC=nAC,CD⊥AB于D,点P为AB边上一动点,PE⊥AC,PF⊥BC,垂足分别为E、F.

(1)若n=2,则
 = ;
= ;(2)当n=3时,连EF、DF,求
 的值;
的值;(3)若
 ,求n的值.
,求n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】南澳大桥是广东省第一座真正意义的跨海大桥,该桥全长约11100m,用科学记数法表示这个数为( ).
A.1.11×104mB.11.1×103 mC.0.111×104mD.1.11×103m
相关试题

