【题目】如图，已知A（﹣2，4），B（4，2），C（2，﹣1）

（1）作△ABC关于x轴的对称图形△A1B1C1 ， 写出点C关于x轴的对称点C1的坐标；
（2）P为x轴上一点，请在图中画出使△PAB的周长最小时的点P并直接写出此时点P的坐标（保留作图痕迹）．

参考答案：

【答案】
（1）解：如图所示，△A1B1C1即为所求.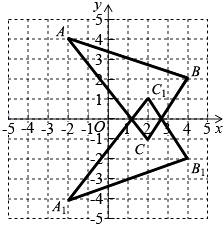

∵点C与点C1关于x轴对称，
又∵点C的坐标为(2, -1)，
∴点C1的坐标为(2, 1)
（2）解：如图所示，点P即为所求.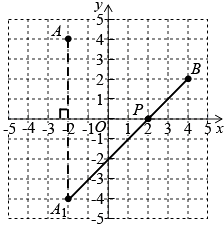

根据上述图形可知，点P的坐标为(2, 0).
【解析】（1）先依据各点的坐标确定出A、B、C的位置，然后利用对称性确定出它们对应点的坐标，从而可画出△A1B1C1 ， 然后，依据关于x轴对称点的横坐标不变，纵坐标互为相反数可确定出点C1的坐标；（2）由AB的长度不变可知当AP+PB有最小值时，三角形的周长最小，作点A关于x轴的对称点，A1 ， 连接A1B交x轴与点P.

关闭