搜索
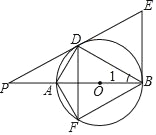
【题目】如图，AB是⊙O的直径，AD、BD是⊙O的弦，且∠PDA=∠1，过点B的切线BE与PD的延长线交于点E．把△PDA沿AD翻折，点P正好落在⊙O的F点上．
（1）证明：PD是⊙O的切线；
（2）求证：DF∥BE；
（3）若PA=2，求四边形BEDF的面积．
参考答案：
【答案】（1）（2）见解析；（3）
【解析】试题分析： 
连接OD． 
根据等量代换得
根据直径所对的圆周角是直角得
即可得到
，即可证明.
由
得
=
,根据垂径定理的推论可得
又BE是切线，即可证明.
根据
可以求出
的长度，证明四边形BEDF是菱形，根据面积公式计算即可.
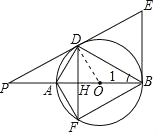
试题解析：证明：连接OD．
∵
∴
∵
∴
∴
∵AB是直径，
∴
∴
，
∴
∴PD是
的切线．
（2）设AB交DF于H．
∵
∴
=
,
∴
∵BE是切线，
∴
，
∴DF∥BE．
（3）
∴
∴
∵
∴
∵
∴
易证四边形BEDF是菱形，面积
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校体育社团在校内开展“最喜欢的体育项目（四项选一项）”调查，对九年级学生随机抽样，并将收集的数据绘制成如图两幅不完整的统计图，请结合统计图解答下列问题：
（1）求本次抽样人数有多少人？
（2）补全条形统计图；
（3）该校九年级共有600名学生，估计九年级最喜欢跳绳项目的学生有多少人？
-
科目： 来源： 题型：
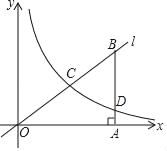
查看答案和解析>>【题目】如图，在平面直角坐标系中，O为坐标原点，经过原点的直线l与反比例函数
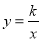（x＞0）的图象交于点C，B是直线l上的点，过点B作BA⊥x轴，垂足为点A，且C是OB中点，已知OA=4，BD=3．（1）用含k的代数式来表示D点的坐标为_____；
（2）求反比例函数的解析式；
（3）连接CD，求四边形OADC的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】中央电视台的“朗读者”节目激发了同学们的读书热情，为了引导学生“多读书，读好书“，某校对八年级部分学生的课外阅读量进行了随机调查，整理调查结果发现，学生课外阅读的本书最少的有5本，最多的有8本，并根据调查结果绘制了不完整的图表，如图所示：
本数（本）
频数（人数）
频率
5
a
0.2
6
18
0.36
7
14
b
8
8
0.16
合计
50
c
我们定义频率=
，比如由表中我们可以知道在这次随机调查中抽样人数为50人课外阅读量为6本的同学为18人，因此这个人数对应的频率就是
=0.36．（1）统计表中的a、b、c的值；
（2）请将频数分布表直方图补充完整；
（3）求所有被调查学生课外阅读的平均本数；
（4）若该校八年级共有600名学生，你认为根据以上调查结果可以估算分析该校八年级学生课外阅读量为7本和8本的总人数为多少吗？请写出你的计算过程．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，O为坐标原点，已知直线y=﹣
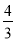x+8与x轴、y轴分别交于A、B两点．直线OD⊥直线AB于点D．现有一点P从点D出发，沿线段DO向点O运动，另一点Q从点O出发，沿线段OA向点A运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到O时，两点都停止．设运动时间为t秒．（1）点A的坐标为_____；线段OD的长为_____．
（2）设△OPQ的面积为S，求S与t之间的函数关系（不要求写出取值范围），并确定t为何值时S的值最大？
（3）是否存在某一时刻t，使得△OPQ为等腰三角形？若存在，写出所有满足条件的t的值；若不存在，则说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，AD∥BC，∠ABC=90°，E是AB上一点，且DE⊥CE．若AD=1，BC=2，CD=3，则CE与DE的数量关系正确的是（ ）
A．CE=
DE B．CE=
DE C．CE=3DE D．CE=2DE -
科目： 来源： 题型：
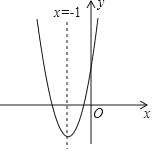
查看答案和解析>>【题目】如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=﹣1，给出下列结论：
①b2=4ac；②abc＞0；③a＞c； ④4a﹣2b+c＞0，其中正确有_____（填序号）．
相关试题
