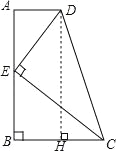
【题目】如图，在四边形ABCD中，AD∥BC，∠ABC=90°，E是AB上一点，且DE⊥CE．若AD=1，BC=2，CD=3，则CE与DE的数量关系正确的是（ ）

A．CE=DE B．CE=DE C．CE=3DE D．CE=2DE

参考答案：

【答案】B．

【解析】

试题分析：过点D作DH⊥BC，利用勾股定理可得AB的长，利用相似三角形的判定定理可得△ADE∽△BEC，设BE=x，由相似三角形的性质可解得x，易得CE，DE 的关系．

过点D作DH⊥BC，由AD=1，BC=2，可求得CH=1，根据勾股定理可得DH=AB==2，

因AD∥BC，∠ABC=90°，可得∠A=90°，即可得∠AED+∠ADE=90°，再由DE⊥CE，可得∠AED+∠BEC=90°，所以∠ADE=∠BEC，即可判定△ADE∽△BEC，由相似三角形的性质可得，设BE=x，则AE=2，即，解得x=，，即CE=，故答案选B．

关闭