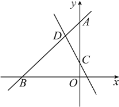
【题目】如图,直线y=kx+4(k≠0)与x轴、y轴分别交于点B,A,直线y=-2x+1与y轴交于点C,与直线y=kx+4交于点D,△ACD的面积是![]() .
.
(1)求直线AB的表达式;
(2)设点E在直线AB上,当△ACE是直角三角形时,请直接写出点E的坐标.
参考答案:
【答案】(1)直线AB的表达式为y=x+4;(2)当△ACE是直角三角形时,点E的坐标为(-3,1)或(-![]() ).
).
【解析】
(1)将=0分别代入两个一次函数表达式中求出点A、C的坐标,进而即可得出AC的长度,再根据三角形的面积公式结合△ACD的面积即可求出点D的横坐标,利用一次函数图象上点的坐标特即可求出点D的坐标,由点D的坐标利用待定系数法即可求出直线AB的表达式;
(2)由直线AB的表达式即可得出△ACE为等腰直角三角形,分∠ACE=90°和∠AEC=90°两种情况考虑,根据点A、C的坐标利用等腰直角三角形的性质即可得出点E的坐标,此题得解.
(1)当x=0时,y=kx+4=4,y=-2x+1=1,
∴A(0,4),C(0,1),
∴AC=3.
∵S△ACD=![]()
![]() AC·(-xD)=-
AC·(-xD)=-![]() xD=
xD=![]() ,
,
∴xD=-1.
当x=-1时,y=-2x+1=3,
∴D(-1,3).
将D(-1,3)代入y=kx+4,得-k+4=3,
解得k=1,
∴直线AB的表达式为y=x+4.
(2)∵直线AB的表达式为y=x+4,
∴△ACE为等腰直角三角形.
如图,当∠ACE=90°时,
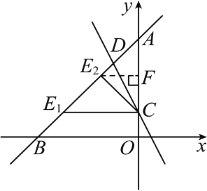
∵A(0,4),C(0,1),AC=3,
∴CE1=3,E1的横坐标为-3.
将x=-3代入y=x+4中,得y=1,
∴E1(-3,1);
当∠AE2C=90°时,
∵A(0,4),C(0,1),AC=3,
过点E2作E2F⊥AC于点F,E2F=AF=FC=![]() AC=
AC=![]() ,
,
∴E2(-![]() ,
,![]() ).
).
综上所述,当△ACE是直角三角形时,点E的坐标为(-3,1)或(-![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了备战初三物理、化学实验操作考试,某校对初三学生进行了模拟训练,物理、化学各有4个不同的操作实验题目,物理用番号①、②、③、④代表,化学用字母a、b、c、d表示,测试时每名学生每科只操作一个实验,实验的题目由学生抽签确定,第一次抽签确定物理实验题目,第二次抽签确定化学实验题目.
(1)请用树形图法或列表法,表示某个同学抽签的各种可能情况.
(2)小张同学对物理的①、②和化学的b、c号实验准备得较好,他同时抽到两科都准备的较好的实验题目的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】情境观察:

如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F.
①写出图1中所有的全等三角形 ;
②线段AF与线段CE的数量关系是 .
问题探究:
如图2,△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E.
求证:AE=2CD.
拓展延伸:
如图3,△ABC中,∠BAC=45°,AB=BC,点D在AC上,∠EDC=
 ∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE.
∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE.要求:请你写出辅助线的作法,并在图3中画出辅助线,不需要证明.
-
科目: 来源: 题型:
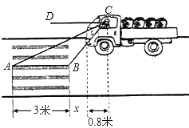
查看答案和解析>>【题目】如图:一辆汽车在一个十字路口遇到红灯刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是∠DCA=30°和∠DCB=60°,如果斑马线的宽度是AB=3米,驾驶员与车头的距离是0.8米,这时汽车车头与斑马线的距离x是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四组条件中,不能判定四边形ABCD是平行四边形的是
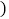
A.
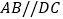 ,
, B.
B. 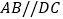 ,
,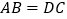
C.
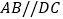 ,
,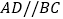 D.
D. 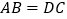 ,
,
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上的点A,O,B,C,D分别表示-3,0,2.5,5,-6.

(1)求B,O两点间的距离;
(2)求A,D两点间的距离;
(3)求C,B两点间的距离;
(4)请观察思考,若点A表示数m,且m<0,点B表示数n,且n>0,用含m,n的代数式表示A,B两点间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF⊥AD,将平行四边形ABCD沿着EF对折.设∠1的度数为n°,则∠C=______.(用含有n的代数式表示)

相关试题

