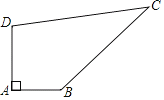
【题目】如图,某开发区有一块四边形的空地ABCD,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,则要投入_____元.
参考答案:
【答案】7200
【解析】
仔细分析题目,需要求得四边形的面积才能求得结果.连接BD,在直角三角形ABD中可求得BD的长,由BD、CD、BC的长度关系可得△DBC为一直角三角形,DC为斜边;由此看,四边形ABCD由Rt△ABD和Rt△DBC构成,则容易求解.
解:连接BD,
在Rt△ABD中,BD2=AB2+AD2=32+42=52,
在△CBD中,CD2=132BC2=122,
而122+52=132,
即BC2+BD2=CD2,
∴∠DBC=90°,
S四边形ABCD=S△BAD+S△DBC=![]() ,
,
=![]() =36.
=36.
所以需费用36×200=7200(元).
故答案为:7200.
-
科目: 来源: 题型:
查看答案和解析>>【题目】文美书店决定用不多于20000元购进甲乙两种图书共1200本进行销售.甲、乙两种图书的进价分别为每本20元、14元,甲种图书每本的售价是乙种图书每本售价的1.4倍,若用1680元在文美书店可购买甲种图书的本数比用1400元购买乙种图书的本数少10本.
(1)甲乙两种图书的售价分别为每本多少元?
(2)书店为了让利读者,决定甲种图书售价每本降低3元,乙种图书售价每本降低2元,问书店应如何进货才能获得最大利润?(购进的两种图书全部销售完.)
-
科目: 来源: 题型:
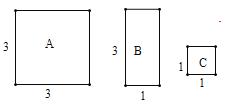
查看答案和解析>>【题目】如图,有A、B、C三种不同型号的卡片,每种卡片各有9张.其中A型卡片是边长为3的正方形,B型卡片是相邻两边长分别为3、1的长方形,C型卡片是边长为1的正方形.从其中取若干张卡片(每种卡片至少取1张),若把取出的这些卡片拼成一个正方形,则所拼正方形的边长的最大值是______.
-
科目: 来源: 题型:
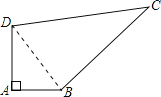
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:
①△BDF≌△DCE;②∠BMD=120°;③△AMH是等边三角形;④S四边形ABCD=
 AM2.
AM2.其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知∠1+∠2=180°,∠3=∠B,
求证:∠AED=∠ACB.

证明:∠1+∠2=180°(已知),∠1+∠4=180°( ),
∴∠2= ( ),
∴AB∥EF( ),
∴∠3= ( ),
∵∠3=∠B(已知),
∴∠B= (等量代换),
∴DE∥BC( ),
∴∠AED=∠ACB( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在OA的位置时俯角∠EOA=30°,在OB的位置时俯角∠FOB=60°,若OC⊥EF,点A比点B高7cm.求:
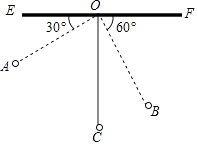
(1)单摆的长度(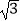 ≈1.7);
≈1.7);
(2)从点A摆动到点B经过的路径长(π≈3.1). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一副创意卡通圆规,图2是其平面示意图,OA是支撑臂,OB是旋转臂,使用时,以点A为支撑点,铅笔芯端点B可绕点A旋转作出圆.已知OA=OB=10cm.

(1)当∠AOB=18°时,求所作圆的半径;(结果精确到0.01cm)
(2)保持∠AOB=18°不变,在旋转臂OB末端的铅笔芯折断了一截的情况下,作出的圆与(1)中所作圆的大小相等,求铅笔芯折断部分的长度.(结果精确到0.01cm)
(参考数据:sin9°≈0.1564,cos9°≈0.9877,sin18°≈0.3090,cos18°≈0.9511,可使用科学计算器)
相关试题

