【题目】如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在OA的位置时俯角∠EOA=30°,在OB的位置时俯角∠FOB=60°,若OC⊥EF,点A比点B高7cm.求: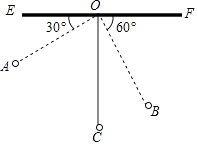
(1)单摆的长度( ![]() ≈1.7);
≈1.7);
(2)从点A摆动到点B经过的路径长(π≈3.1).
参考答案:
【答案】
(1)
解:如图,过点A作AP⊥OC于点P,过点B作BQ⊥OC于点Q,
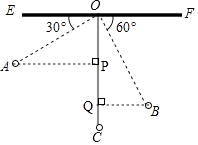
∵∠EOA=30°、∠FOB=60°,且OC⊥EF,
∴∠AOP=60°、∠BOQ=30°,
设OA=OB=x,
则在Rt△AOP中,OP=OAcos∠AOP= ![]() x,
x,
在Rt△BOQ中,OQ=OBcos∠BOQ= ![]() x,
x,
由PQ=OQ﹣OP可得 ![]() x﹣
x﹣ ![]() x=7,
x=7,
解得:x=7+7 ![]() ≈18.9(cm),
≈18.9(cm),
答:单摆的长度约为18.9cm
(2)
解:由(1)知,∠AOP=60°、∠BOQ=30°,且OA=OB=7+7 ![]() ,
,
∴∠AOB=90°,
则从点A摆动到点B经过的路径长为 ![]() ≈29.295,
≈29.295,
答:从点A摆动到点B经过的路径长为29.295cm
【解析】(1)作AP⊥OC、BQ⊥OC,由题意得∠AOP=60°、∠BOQ=30°,设OA=OB=x,根据三角函数得OP=OAcos∠AOP= ![]() x、OQ=OBcos∠BOQ=
x、OQ=OBcos∠BOQ= ![]() x,由PQ=OQ﹣OP可得关于x的方程,解之可得;(2)由(1)知∠AOB=90°、OA=OB=7+7
x,由PQ=OQ﹣OP可得关于x的方程,解之可得;(2)由(1)知∠AOB=90°、OA=OB=7+7 ![]() ,利用弧长公式求解可得.
,利用弧长公式求解可得.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:
①△BDF≌△DCE;②∠BMD=120°;③△AMH是等边三角形;④S四边形ABCD=
 AM2.
AM2.其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
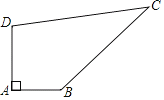
查看答案和解析>>【题目】如图,某开发区有一块四边形的空地ABCD,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,则要投入_____元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知∠1+∠2=180°,∠3=∠B,
求证:∠AED=∠ACB.

证明:∠1+∠2=180°(已知),∠1+∠4=180°( ),
∴∠2= ( ),
∴AB∥EF( ),
∴∠3= ( ),
∵∠3=∠B(已知),
∴∠B= (等量代换),
∴DE∥BC( ),
∴∠AED=∠ACB( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一副创意卡通圆规,图2是其平面示意图,OA是支撑臂,OB是旋转臂,使用时,以点A为支撑点,铅笔芯端点B可绕点A旋转作出圆.已知OA=OB=10cm.

(1)当∠AOB=18°时,求所作圆的半径;(结果精确到0.01cm)
(2)保持∠AOB=18°不变,在旋转臂OB末端的铅笔芯折断了一截的情况下,作出的圆与(1)中所作圆的大小相等,求铅笔芯折断部分的长度.(结果精确到0.01cm)
(参考数据:sin9°≈0.1564,cos9°≈0.9877,sin18°≈0.3090,cos18°≈0.9511,可使用科学计算器) -
科目: 来源: 题型:
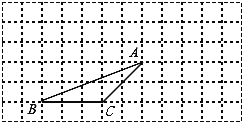
查看答案和解析>>【题目】如图,△ABC的顶点都在方格纸的格点上,将△ABC向右平移4格,再向上平移2格,其中每个格子的边长为1个单位长度。
⑴在图中画出平移后的△A′B′C′;
⑵若连接AA′、CC′,则这两条线段的关系是 ;
⑶作△ABC的高AD,并求△ABC的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°.
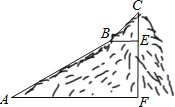
(1)求AB段山坡的高度EF;
(2)求山峰的高度CF.(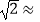 1.414,CF结果精确到米)
1.414,CF结果精确到米)
相关试题

