【题目】在平面直角坐标系中,O是坐标原点,点A的坐标是(﹣4,0),点B的坐标是(0,b)(b>0),点P是直线AB上的一个动点,记点P关于y轴对称的点为P′.
(1)当b=3时(如图1),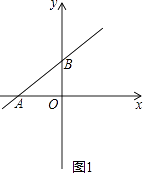
①求直线AB的函数表达式.
(2)②在x轴上找一点Q(点O除外),使△APQ与△AOB全等,直接写出点Q的所有坐标
(3)若点P在第一象限(如图2),设点P的横坐标为a,作PC⊥x轴于点C,连结AP′,CP′.当△ACP′是以点P′为直角顶点的等腰直角三角形时,求出a,b的值.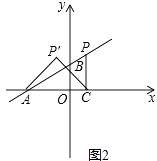
(4)当线段OP′恰好被直线AB垂直平分时(如图3),直接写出b= . 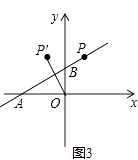
参考答案:
【答案】
(1)
解:设直线AB的函数表达式为y=kx+b,
∵点A的坐标是(﹣4,0),点B的坐标是(0,3)
∴有 ![]() ,解得:
,解得: ![]() .
.
故直线AB的函数表达式为y= ![]() x+3.
x+3.
(2)(﹣9,0)、(﹣8,0)或(1,0)
(3)
解:过P′作PD⊥x轴于点D,如图所示.
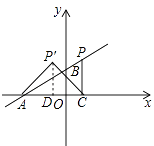
∵点A的坐标是(﹣4,0),点B的坐标是(0,b)(b>0),
∴直线AB的斜率为 ![]() =
= ![]() ,
,
即直线AB的解析式为y= ![]() x+b.
x+b.
∵点P在直线AB上,
∴点P的坐标为(a, ![]() a+b),则点P′的坐标为(﹣a,
a+b),则点P′的坐标为(﹣a, ![]() a+b),点C的坐标为(a,0),点D的坐标为(﹣a,0),
a+b),点C的坐标为(a,0),点D的坐标为(﹣a,0),
∴P′D= ![]() a+b,AC=a+4,AD=4﹣a.
a+b,AC=a+4,AD=4﹣a.
∵点P为第一象限的点,
∴a>0.
∵△ACP′是以点P′为直角顶点的等腰直角三角形,
∴有 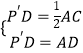 ,即
,即 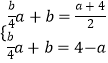 ,
,
解得: ![]()
(4)![]()
【解析】解:(1)①设直线AB的函数表达式为y=kx+b,
∵点A的坐标是(﹣4,0),点B的坐标是(0,3)
∴有 ![]() ,解得:
,解得: ![]() .
.
故直线AB的函数表达式为y= ![]() x+3.
x+3.
②∵点P是直线AB上的一个动点,点Q为x轴上一点(点O除外),
∴设点Q的坐标为(m,0),∠PAQ=∠BAO,
∴AQ=|m+4|.
在Rt△AOB中,AO=4,BO=3,AB= ![]() =5.
=5.
△APQ与△AOB全等有两种情况:
当AQ=AO时,即|m+4|=4,
解得:m=0(舍去),或m=﹣8,
此时点Q的坐标为(﹣8,0);
当AQ=AB时,即|m+4|=5,
解得:m=﹣9,或m=1,
此时点Q的坐标为(﹣9,0)或(1,0).
综上所述:点Q的所有坐标为(﹣9,0),(﹣8,0)或(1,0).
所以答案是:(﹣9,0),(﹣8,0)或(1,0).(4)由(3)可知:点P的坐标为(a, ![]() a+b),则点P′的坐标为(﹣a,
a+b),则点P′的坐标为(﹣a, ![]() a+b),直线AB的解析式为y=
a+b),直线AB的解析式为y= ![]() x+b.
x+b.
则OP′的中点坐标为(﹣ ![]() ,
, ![]() ),直线OP′的斜率为
),直线OP′的斜率为 ![]() =﹣
=﹣ ![]() ﹣
﹣ ![]() .
.
∵线段OP′恰好被直线AB垂直平分,
∴有  ,
,
解得: 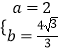 ,或
,或  (舍去).
(舍去).
所以答案是: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;并求出自变量x的取值范围;
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在实数范围内因式分解:2x3+8x2+8x=_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(﹣4,0),把△AOB平移,使点A移至点D(2,1),点O、B的对应点分别是点E、F.
(1)请在图中画出△DEF,并写出点E,F的坐标.
(2)点P(﹣1,1)在△AOB内,当△AOB平移到△DEF位置时,求点P的对应点P′的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】商店对某种手机的售价作了调整,按原售价的 8 折出售,此时的利润率为 14%,若此种手机的进价为 1200 元,设该手机的原售价为 x 元,则下列方程正确的是( )
A. 0.8x﹣1200=1200×14% B. 0.8x﹣1200=14%x
C. x﹣0.8x=1200×14% D. 0.8x﹣1200=14%×0.8x
-
科目: 来源: 题型:
查看答案和解析>>【题目】火灾猛于虎!据应急管理部统计,2018年全国共接报火灾23.7万起,死亡1407人,伤798人,直接财产损失36.75亿元,其中36.75亿元用科学记数法表示正确的是( )
A. 3.675×109元B. 0.3675×1010元
C. 3.675×108元D. 36.75×108元
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形ABCD在坐标平面内,点A的坐标是A(2,1),且边AB、CD与x轴平行,边AD、BC与x轴平行,点B、C的坐标分别为B(a,1),C(a,c),且a、c满足关系式.c=
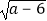 +
+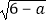 +3
+3
(1)求B、C、D三点的坐标;
(2)怎样平移,才能使A点与原点重合?平移后点B、C、D的对应分别为B1C1D1 , 求四边形OB1C1D1的面积;
(3)平移后在x轴上是否存在点P,连接PD,使S△COP=S四边形OBCD?若存在这样的点P,求出点P的坐标;若不存在,试说明理由.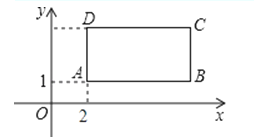
相关试题

