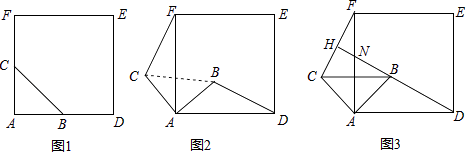
【题目】如图1,2,3分别以△ABC的AB和AC为边向△ABC外作正三角形(等边三角形)、正四边形(正方形)、正五边形,BE和CD相交于点O.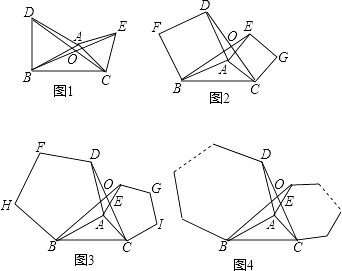
(1)在图1中,求证:△ABE≌△ADC.
(2)由(1)证得△ABE≌△ADC,由此可推得在图1中∠BOC=120°,请你探索在图2中,∠BOC的度数,并说明理由或写出证明过程.
(3)填空:在上述(1)(2)的基础上可得在图3中∠BOC=(填写度数).
(4)由此推广到一般情形(如图4),分别以△ABC的AB和AC为边向△ABC外作正n边形,BE和CD仍相交于点O,猜想得∠BOC的度数为(用含n的式子表示).
参考答案:
【答案】
(1)
证明:如图1,∵△ABD和△ACE是等边三角形,
∴AB=AD,AC=AE,∠DAB=∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
即∠DAC=∠BAE,
∴△ABE≌△ADC

(2)
证明:如图2,∠BOC=90°,理由是:
∵四边形ABFD和四边形ACGE都是正方形,
∴AB=AD,AC=AE,∠DAB=∠EAC=90°,
∴∠BAE=∠DAC,
∴△ADC≌△ABE,
∴∠BEA=∠DCA,
∵∠EAC=90°,
∴∠AMC+∠DCA=90°,
∵∠BOC=∠OME+∠BEA=∠AMC+∠DCA,
∴∠BOC=90°
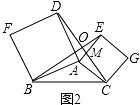
(3)72°
(4)![]()
【解析】证明:(3)如图3,同理得:△ADC≌△ABE,
∴∠BEM=∠DCA,
∵∠BOC=∠BEM+∠OME=∠DCA+∠AMC,
∵正五边形ACIGE,
∴∠EAC=180°﹣ ![]() =108°,
=108°,
∴∠DCA+∠AMC=72°,
∴∠BOC=72°;
故答案为:72°;
4)如图4,∠BOC的度数为 ![]() ,理由是:
,理由是:
同理得:△ADC≌△ABE,
∴∠BEA=∠DCA,
∵∠BOC=∠BEA+∠OME=∠DCA+∠AMC,
∵正n边形AC…E,
∴∠EAC=180°﹣ ![]() ,
,
∴∠DCA+∠AMC=180°﹣(180﹣ ![]() )°,
)°,
∴∠BOC= ![]() .
.
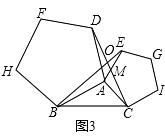
(1)根据等边三角形证明AB=AD,AC=AE,再利用等式性质得∠DAC=∠BAE,根据SAS得出△ABE≌△ADC;(2)根据正方形性质证明△ABE≌△ADC,得∠BEA=∠DCA,再由正方形ACEG的内角∠EAC=90°和三角形外角和定理得∠BOC=90°;(3)根据正五边形的性质证明:△ADC≌△ABE,再计算五边形每一个内角的度数为108°,由三角形外角定理求出∠BOC=72°;(4)根据正n边形的性质证明:△ADC≌△ABE,再计算n边形每一个内角的度数为180°﹣ ![]() ,由三角形外角定理求出∠BOC=
,由三角形外角定理求出∠BOC= ![]() .本题是四边形的综合题,考查了全等三角形、等边三角形、正四边形等图形的性质,关键是利用正n边形各边相等证明两三角形全等,运用了类比的方法,同时还要熟练掌握正n边形每一个内角的求法:可以利用外角和求,也可以利用内角和求;根据三角形的一个外角等于与它不相邻的两个内角和列式并综合对顶角相等分别得出结论.
.本题是四边形的综合题,考查了全等三角形、等边三角形、正四边形等图形的性质,关键是利用正n边形各边相等证明两三角形全等,运用了类比的方法,同时还要熟练掌握正n边形每一个内角的求法:可以利用外角和求,也可以利用内角和求;根据三角形的一个外角等于与它不相邻的两个内角和列式并综合对顶角相等分别得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明用的练习本,一般在甲、乙两家文具店购买,已知两家文具店的标价都是每本1元,但甲文具店的优惠条件是一次购买10本以上,从第11本起按标价的70%卖;乙文具店的优惠条件是全部按八五折优惠.
(1)若小明打算买30本,到哪家店购买省钱?
(2)小明现有38元钱,最多可买多少本练习本?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,∠BAC=2∠DAE=2α.
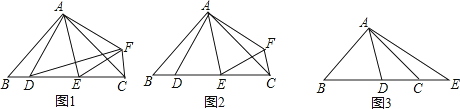
(1)如图1,若点D关于直线AE的对称点为F,求证:△ADF∽△ABC;
(2)如图2,在(1)的条件下,若α=45°,求证:DE2=BD2+CE2;
(3)如图3,若α=45°,点E在BC的延长线上,则等式DE2=BD2+CE2还能成立吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.
(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明,若不成立,请说明理由;
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长BD交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3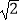 时,求线段DH的长.
时,求线段DH的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在学习了图形的旋转知识后,数学兴趣小组的同学们又进一步对图形旋转前后的线段之间、角之间的关系进行了探究.
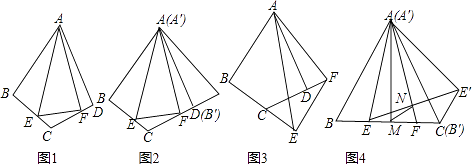
(一)尝试探究
如图1,在四边形ABCD中,AB=AD,∠BAD=60°,∠ABC=∠ADC=90°,点E、F分别在线段BC、CD上,∠EAF=30°,连接EF.
(1)如图2,将△ABE绕点A逆时针旋转60°后得到△A′B′E′(A′B′与AD重合),请直接写出∠E′AF=度,线段BE、EF、FD之间的数量关系为 .
(2)如图3,当点E、F分别在线段BC、CD的延长线上时,其他条件不变,请探究线段BE、EF、FD之间的数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】市政府建设一项水利工程,某运输公司承担运送总量为106m3的土石方任务,该公司有甲、乙两种型号的卡车共100辆,甲型车平均每天可以运送土石方80m3,乙型车平均每天可以运送土石方120m3,计划100天完成运输任务.
(1)该公司甲、乙两种型号的卡车各有多少台?
(2)如果该公司用原有的100辆卡车工作了40天后,由于工程进度的需要,剩下的所有运输任务必须在50天内完成,在甲型卡车数量不变情况下,公司至少应增加多少辆乙型卡车?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市南县大力发展农村旅游事业,全力打造“洞庭之心湿地公园”,其中罗文村的“花海、涂鸦、美食”特色游享誉三湘,游人如织.去年村民罗南洲抓住机遇,返乡创业,投入20万元创办农家乐(餐饮+住宿),一年时间就收回投资的80%,其中餐饮利润是住宿利润的2倍还多1万元.
(1)求去年该农家乐餐饮和住宿的利润各为多少万元?
(2)今年罗南洲把去年的餐饮利润全部用于继续投资,增设了土特产的实体店销售和网上销售项目.他在接受记者采访时说:“我预计今年餐饮和住宿的利润比去年会有10%的增长,加上土特产销售的利润,到年底除收回所有投资外,还将获得不少于10万元的纯利润.”请问今年土特产销售至少有多少万元的利润?
相关试题

