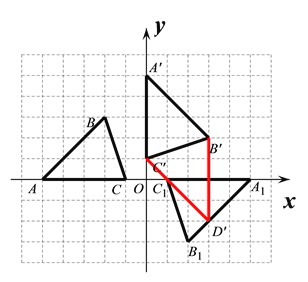
【题目】已知△ABC的三个顶点的坐标分别为A(﹣5,0)、B(﹣2,3)、C(﹣1,0)
(1)画出△ABC关于坐标原点O成中心对称的△A1B1C1;
(2)将△ABC绕坐标原点O顺时针旋转90°,画出对应的△A′B′C′,
(3)若以A′、B′、C′、D′为顶点的四边形为平行四边形,请直接写出在第四象限中的D′坐标 .

参考答案:
【答案】(1)见解析;(2)见解析;(3)(3,-2)
【解析】整体分析:
分别根据中心对称的性质与旋转的性质画出符合条件的图形,由点A′到点B′的平移规律求出点D′的坐标.
解:(1)△ABC关于坐标原点O成中心对称的△A1B1C1,如图所示:
(2)如图所示:
(3)如图,因为从点A′到点B′是向下平移3个单位,再向右平移3个单位,所以把点C′向下平移3个单位,再向右平移3个单位后即是点D′的坐标,根据旋转的性质得C′(0,1),故D′(3,-2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
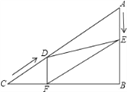
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形。若
 ,AB=2,则图中阴影部分的面积为( )
,AB=2,则图中阴影部分的面积为( )
A. 12-4
 B. 5 C. 12-4
B. 5 C. 12-4 D. 6
D. 6 -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,若M=a+b﹣c,N=4a﹣2b+c,P=2a﹣b.则M,N,P中,值小于0的数有( )
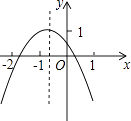
A.3个
B.2个
C.1个
D.0个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=
 x与双曲线y=
x与双曲线y= 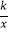 (k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线y=
(k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线y= 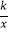 (k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为 .
(k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为 . 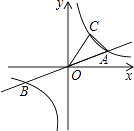
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解下面内容,并解决问题:
善于思考的小明在学习《实数》一章后,自己探究出了下面的两个结论:
①
 ,
, ,
, 和
和 都是9×4的算术平方根,
都是9×4的算术平方根,而9×4的算术平方根只有一个,所以
 =
= .
.②
 ,
, ,
, 和
和 都是9×16的算术平方根,
都是9×16的算术平方根,而9×16的算术平方根只有一个,所以 .
请解决以下问题:
(1)请仿照①帮助小明完成②的填空,并猜想:一般地,当a≥0,b≥0时,
 与
与 、
、 之间的大小关系是怎样的?
之间的大小关系是怎样的?(2)再举一个例子,检验你猜想的结果是否正确.
(3)运用以上结论,计算:
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学在创建“特色校园”的活动中,将本校的办学理念做成宣传牌(AB),放置在教学楼的顶部(如图所示).小明在操场上的点D处,用1米高的测角仪CD,从点C测得宣传牌的底部B的仰角为37°,然后向教学楼正方向走了4米到达点F处,又从点E测得宣传牌的顶部A的仰角为45°.已知教学楼高BM=17米,且点A,B,M在同一直线上,求宣传牌AB的高度(结果精确到0.1米,参考数据:
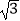 ≈1.73,sin37°≈0.60,cos37°≈0.81,tan37°≈0.75).
≈1.73,sin37°≈0.60,cos37°≈0.81,tan37°≈0.75).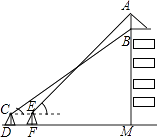
相关试题

