【题目】如图,已知直线y= ![]() x与双曲线y=
x与双曲线y= ![]() (k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线y=
(k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线y= ![]() (k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为 .
(k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为 . 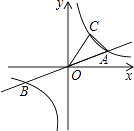
参考答案:
【答案】(2,4)或(8,1)
【解析】解:∵点B(﹣4,﹣2)在双曲线y= ![]() 上, ∴
上, ∴ ![]() =﹣2,
=﹣2,
∴k=8,
根据中心对称性,点A、B关于原点对称,
所以,A(4,2),
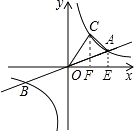
如图,过点A作AE⊥x轴于E,过点C作CF⊥x轴于F,设点C的坐标为(a, ![]() ),
),
若S△AOC=S△COF+S梯形ACFE﹣S△AOE ,
= ![]() ×8+
×8+ ![]() ×(2+
×(2+ ![]() )(4﹣a)﹣
)(4﹣a)﹣ ![]() ×8,
×8,
=4+ ![]() ﹣4,
﹣4,
= ![]() ,
,
∵△AOC的面积为6,
∴ ![]() =6,
=6,
整理得,a2+6a﹣16=0,
解得a1=2,a2=﹣8(舍去),
∴ ![]() =
= ![]() =4,
=4,
∴点C的坐标为(2,4).
若S△AOC=S△AOE+S梯形ACFE﹣S△COF= ![]() ,
,
∴ ![]() =6,
=6,
解得:a=8或a=﹣2(舍去)
∴点C的坐标为(8,1).
所以答案是:(2,4)或(8,1).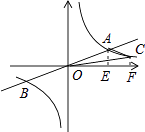
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形。若
 ,AB=2,则图中阴影部分的面积为( )
,AB=2,则图中阴影部分的面积为( )
A. 12-4
 B. 5 C. 12-4
B. 5 C. 12-4 D. 6
D. 6 -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,若M=a+b﹣c,N=4a﹣2b+c,P=2a﹣b.则M,N,P中,值小于0的数有( )
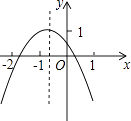
A.3个
B.2个
C.1个
D.0个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的三个顶点的坐标分别为A(﹣5,0)、B(﹣2,3)、C(﹣1,0)
(1)画出△ABC关于坐标原点O成中心对称的△A1B1C1;
(2)将△ABC绕坐标原点O顺时针旋转90°,画出对应的△A′B′C′,
(3)若以A′、B′、C′、D′为顶点的四边形为平行四边形,请直接写出在第四象限中的D′坐标 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解下面内容,并解决问题:
善于思考的小明在学习《实数》一章后,自己探究出了下面的两个结论:
①
 ,
, ,
, 和
和 都是9×4的算术平方根,
都是9×4的算术平方根,而9×4的算术平方根只有一个,所以
 =
= .
.②
 ,
, ,
, 和
和 都是9×16的算术平方根,
都是9×16的算术平方根,而9×16的算术平方根只有一个,所以 .
请解决以下问题:
(1)请仿照①帮助小明完成②的填空,并猜想:一般地,当a≥0,b≥0时,
 与
与 、
、 之间的大小关系是怎样的?
之间的大小关系是怎样的?(2)再举一个例子,检验你猜想的结果是否正确.
(3)运用以上结论,计算:
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学在创建“特色校园”的活动中,将本校的办学理念做成宣传牌(AB),放置在教学楼的顶部(如图所示).小明在操场上的点D处,用1米高的测角仪CD,从点C测得宣传牌的底部B的仰角为37°,然后向教学楼正方向走了4米到达点F处,又从点E测得宣传牌的顶部A的仰角为45°.已知教学楼高BM=17米,且点A,B,M在同一直线上,求宣传牌AB的高度(结果精确到0.1米,参考数据:
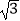 ≈1.73,sin37°≈0.60,cos37°≈0.81,tan37°≈0.75).
≈1.73,sin37°≈0.60,cos37°≈0.81,tan37°≈0.75).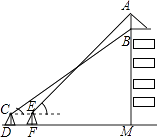
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(2a﹣12,1﹣a)位于第三象限,点Q(x,y)位于第二象限且是由点P向上平移一定单位长度得到的.
(1)若点P的纵坐标为﹣3,试求出a的值;
(2)在(1)题的条件下,试求出符合条件的一个点Q的坐标;
(3)若点P的横、纵坐标都是整数,试求出a的值以及线段PQ长度的取值范围.

相关试题

