【题目】如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,O是AB上一点,以OA为半径的⊙O经过点D。
(1)求证:BC是⊙O切线;
(2)若BD=5,DC=3,求AC的长。
参考答案:
【答案】
(1)证明:连接OD;

∵AD是∠BAC的平分线,
∴∠1=∠3.
∵OA=OD,
∴∠1=∠2.
∴∠2=∠3.
∴OD∥AC.
∴∠ODB=∠ACB=90°.
∴OD⊥BC.
∴BC是⊙O切线.
(2)蛸:过点D作DE⊥AB,

∵AD是∠BAC的平分线,
∴CD=DE=3.
在Rt△BDE中,∠BED=90°,
由勾股定理得:BE= ![]() =4,
=4,
∵∠BED=∠ACB=90°,∠B=∠B,
∴△BDE∽△BAC.
∴ ![]() .
.
∴ ![]() .
.
∴AC=6.
【解析】(1)要证BC是⊙O切线.添加辅助线连接OD,证明OD⊥BC。先根据角平分线的定义及等腰三角形的性质,证出OD∥AC(或∠2+∠ADC=90°),再利用平行线的性质得出OD⊥BC,即可证得结论。
(2)过点D作DE⊥AB,根据角平分线上的点到角两边的距离相等,得出CD=DE=3,再利用勾股定理求出BE的长,再根据两组角对应相等的两三角形相似,得出△BDE∽△BAC。得出对应边成比例,建立方程,求解即可;或证明AE=AC,在Rt△ABC中,利用勾股定理求出AC即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2+2x﹣1.
(1)写出它的顶点坐标;
(2)当x取何值时,y随x的增大而增大;
(3)求出图象与x轴的交点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数y =
 的图象经过点A(1,-3),一次函数y =kx +b的图象经过点A与点C(0,-4),且与反比例函数的图象相交于另一点B.试确定点B的坐标.
的图象经过点A(1,-3),一次函数y =kx +b的图象经过点A与点C(0,-4),且与反比例函数的图象相交于另一点B.试确定点B的坐标.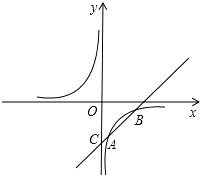
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.
(1)判断∠ABE与∠ACD的数量关系,并说明理由;
(2)求证:过点A、F的直线垂直平分线段BC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋中装有5个黄球,13个黑球和22个红球,这些球除颜色外其他都相同.
(1)求从袋中摸出一个球是黄球的概率.
(2)现在从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后,使从袋中摸出一个球是黄球的概率不小于 ,问:至少取出多少个黑球?
,问:至少取出多少个黑球? -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于
 轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C和△A2B2C2,它们是否关于某直线对称?若是,请用实线条画出对称轴。

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知一个角的补角比它的余角的 3 倍大 30°,求这个角的度数;
(2)如图,点 C、D在线段 AB上, D是线段 AB的中点, AC
 AD , AB6,求线段 CD的长.
AD , AB6,求线段 CD的长.
相关试题

