【题目】如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于点F.
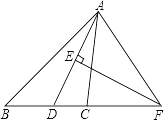
(1)求证:∠FAD=∠FDA;
(2)若∠B=50°,求∠CAF的度数.
参考答案:
【答案】(1)见解析;(2)∠CAF=50°.
【解析】
(1)根据EF垂直平分AD,则可得AF=DF,根据等腰三角形的性质可得结论;
(2)由AD是∠BAC的平分线,可得∠BAD=∠DAC.根据∠FDA=∠BAD+∠B,∠FAD=∠DAC+∠CAF,可证∠B=∠CAF,从而可求出结论.
(1)证明:∵EF是AD的垂直平分线,
∴AF=DF.
∴∠FAD=∠FDA.
(2)∵AD平分∠BAC,
∴∠BAD=∠DAC.
∵∠FDA=∠BAD+∠B,∠FAD=∠DAC+∠CAF,
由(1)知∠FAD=∠FDA,
∴∠B=∠CAF.
∵∠B=50°,
∴∠CAF=50°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解市民私家车出行的情况,某市交通管理部门对拥有私家车的市民进行随机抽样调查、其中一个问题是“你平均每天开车出行的时间是多少”共有4个选项:A、1小时以上(不含1小时);B:0.5-1小时(不含0.5小时);C:0-0.5小时(不含0小时);D,不开车.图1、2是根据调査结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:
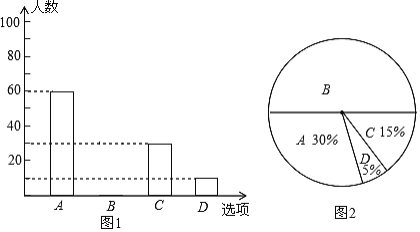
(1)本次一共调查了______名市民;
(2)在图1中将选项B的部分补充完整,并求图2中,A类所对应扇形圆心角α的度数;
(3)若该市共有200万私家车,你估计全市可能有多少私家车平均每天开车出行的时间在1小时以上?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,AE平分∠BAD交边BC于E,DF平分∠ADC交边BC于F,若AD=11,EF=5,则AB=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市计划购进甲、乙两种型号的台灯1000台,这两种型号台灯的进价、售价如下表:
进价(元/台)
售价(元/台)
甲种
45
55
乙种
60
80
(1)如果超市的进货款为54000元,那么可计划购进甲、乙两种型号的台灯各多少台?
(2)为确保乙种型号的台灯销售更快,超市决定对乙种型号的台灯打折销售,且保证乙种型号台灯的利润率为
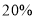 ,问乙种型号台灯需打几折?
,问乙种型号台灯需打几折? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A D C F在同一直线上,AB=DE,AD=CF,添加下列条件后,仍不能判断△ABC≌△DEF的是 ( )
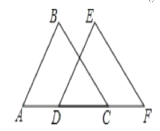
A. BC=EFB. ∠A=∠EDFC. AB∥DED. ∠BCA=∠F
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:OB、OC、OM、ON是∠AOD内的射线.
(1)如图1,若∠AOD=156°,OM平分∠AOB,ON平分∠BOD,∠BOD=96°,则∠MON的度数为 .
(2)如图2,若∠AOD=m°,∠NOC=23°,OM平分∠AOB,ON平分∠BOD,求∠COM的度数(用m的式子表示);
(3)如图3,若∠AOD=156°,∠BOC=22°,∠AOB=30°,OM平分∠AOC,ON平分∠BOD,当∠BOC在∠AOD内绕着点O以2°/秒的速度逆时针旋转t秒时,∠AOM和∠DON中的一个角的度数恰好是另一个角的度数的两倍,求t的值.

相关试题

