【题目】已知:OB、OC、OM、ON是∠AOD内的射线.
(1)如图1,若∠AOD=156°,OM平分∠AOB,ON平分∠BOD,∠BOD=96°,则∠MON的度数为 .
(2)如图2,若∠AOD=m°,∠NOC=23°,OM平分∠AOB,ON平分∠BOD,求∠COM的度数(用m的式子表示);
(3)如图3,若∠AOD=156°,∠BOC=22°,∠AOB=30°,OM平分∠AOC,ON平分∠BOD,当∠BOC在∠AOD内绕着点O以2°/秒的速度逆时针旋转t秒时,∠AOM和∠DON中的一个角的度数恰好是另一个角的度数的两倍,求t的值.

参考答案:
【答案】(1)78°;(2)![]() ;(3) 当
;(3) 当![]() 或
或![]() 时,∠AOM和∠DON中的一个角的度数恰好是另一个角的度数的两倍
时,∠AOM和∠DON中的一个角的度数恰好是另一个角的度数的两倍
【解析】
(1)由OM平分∠AOB,ON平分∠BOD,得∠BOM=30°,∠BON=48°,进而即可求解;
(2)由角平分线的定义得∠BOM=![]() ∠AOB,∠BON=
∠AOB,∠BON=![]() ∠BOD,进而得∠MON=
∠BOD,进而得∠MON=![]() ,即可求解;
,即可求解;
(3)由题意得:∠AOM═(26+t) °,∠DON=(63﹣t) °,根据∠AOM和∠DON中的一个角的度数恰好是另一个角的度数的两倍,列出关于t的方程,即可求解.
(1)∵∠AOD=156°,∠BOD=96°,
∴∠AOB=156°﹣96°=60°,
∵OM平分∠AOB,ON平分∠BOD,
∴∠BOM=30°,∠BON=48°,
∴∠MON=∠BOM+∠BON=78°;
(2)∵OM平分∠AOB,ON平分∠BOD,
∴∠BOM=![]() ∠AOB,∠BON=
∠AOB,∠BON=![]() ∠BOD,
∠BOD,
∵∠MON=∠BOM+∠BON=![]() (∠AOB+∠BOD)=
(∠AOB+∠BOD)= ![]() ∠AOD=
∠AOD=![]() ,
,
∴![]() ;
;
(3)∵∠BOC在∠AOD内绕点O以2°/秒的速度逆时针旋转t秒,
∴∠AOC=(52+2t) °,∠BOD=(126﹣2t) °,
∵OM平分∠AOC,ON平分∠BOD,
∴∠AOM═(26+t) °,∠DON=(63﹣t) °,
当∠AOM=2∠DON时,26+t=2(63﹣t),则![]() ;
;
当∠DON=2∠AOM时,63﹣t=2(26+t),则t=![]() .
.
故当![]() 或
或![]() 时,∠AOM和∠DON中的一个角的度数恰好是另一个角的度数的两倍,
时,∠AOM和∠DON中的一个角的度数恰好是另一个角的度数的两倍,
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于点F.
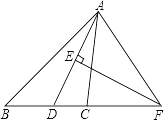
(1)求证:∠FAD=∠FDA;
(2)若∠B=50°,求∠CAF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A D C F在同一直线上,AB=DE,AD=CF,添加下列条件后,仍不能判断△ABC≌△DEF的是 ( )
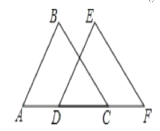
A. BC=EFB. ∠A=∠EDFC. AB∥DED. ∠BCA=∠F
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知D,E分别为边BC,AD的中点,且S△ABC=4 cm2,则△BEC的面积为( )

A. 2 cm2 B. 1 cm2 C. 0.5 cm2 D. 0.25 cm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
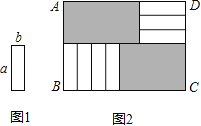
A.a=
 bB.a=3bC.a=
bB.a=3bC.a= bD.a=4b
bD.a=4b -
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们经济收入的不断提高,汽车已越来越多地进入到各个家庭.某大型超市为缓解停车难问题,建筑设计师提供了楼顶停车场的设计示意图.按规定,停车场坡道口上坡要张贴限高标志,以便告知车辆能否安全驶入.如图,地面所在的直线ME与楼顶所在的直线AC是平行的,CD的厚度为0.5m,求出汽车通过坡道口的限高DF的长(结果精确到0.1m,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53).

相关试题

