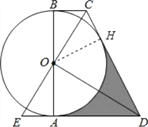
【题目】如图,AB为⊙O的直径,BC、AD是⊙O的切线,过O点作EC⊥OD,EC交BC于C,交直线AD于E.
(1)求证:CD是⊙O的切线;
(2)若AE=1,AD=3,求阴影部分的面积.

参考答案:
【答案】(1)见解析;(2) 3![]() ﹣π;
﹣π;
【解析】试题分析:(1)首先作OH⊥CD,垂足为H,由BC、AD是⊙O的切线,易证得△BOC≌△AOE(ASA),继而可得OD是CE的垂直平分线,则可判定DC=DE,即可得OD平分∠CDE,则可得OH=OA,证得CD是⊙O的切线;
(2)首先证得△AOE∽△ADO,然后由相似三角形的对应边成比例,求得OA的长,然后利用三角函数的性质,求得∠DOA的度数,继而求得答案.
试题解析:
(1)证明:作OH⊥CD,垂足为H,
∵BC、AD是⊙O的切线,
∴∠CBO=∠OAE=90°,
在△BOC和△AOE中,![]() ,
,
∴△BOC≌△AOE(ASA),
∴OC=OE,
又∵EC⊥OD,
∴DE=DC,
∴∠ODC=∠ODE,
∴OH=OA,
∴CD是⊙O的切线;
(2)∵∠E+∠AOE=90°,∠DOA+∠AOE=90°,
∴∠E=∠DOA,
又∵∠OAE=∠ODA=90°,
∴△AOE∽△ADO,
∴![]() =
=![]() ,
,
∴OA2=EAAD=1×3=3,
∵OA>0,
∴OA=![]() ,
,
∴tanE=![]() =
=![]() ,
,
∴∠DOA=∠E=60°,
∵DA=DH,∠OAD=∠OHD=90°,
∴∠DOH=∠DOA=60°,
∴S阴影部分=![]() ×3×
×3×![]() +
+![]() ×3×
×3×![]() ﹣
﹣![]() =3
=3![]() ﹣π.
﹣π.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则
 的值等于 .
的值等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式ax2﹣4axy+4ay2分解因式的结果为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的一个内角是68°,则顶角是( )
A. 68° B. 44° C. 68°或44° D. 68°或112°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某新型感冒病毒的直径约为0.000000823米,将0.000000823用科学记数法表示为___________
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学今年年初开学后打算招聘一名数学老师,对三名前来应聘的数学老师A、B、C进行了考核,他们的笔试成绩和说课成绩(单位:分)分别用了两种方式进行了统计,如表和图1,
A
B
C
笔试
85
95
90
说课
80
85
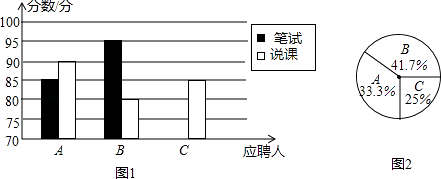
(1)请将表和图1的空缺部分补充完整;
(2)应聘的最后一个程序是由该校的24名数学教师进行投票,三位应聘者的得票情况如图2(没有弃权票,该校的每位教师只能选一位应聘教师),请计算每人的得票数(得票数可是整数哟)
(3)若每票计1分,该校将笔试、说课、得票三项测试得分按3:4:3的比例 确定个人成绩,请计算三位应聘者的最后成绩,并根据成绩判断谁能应聘成功. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为r,圆心O到直线l的距离为d.若直线l与⊙O有交点,则下列结论正确的是( )
A.d=rB.d≤rC.d≥rD.d<r
相关试题

