搜索
【题目】如图，在正方形ABCD中，点E，N，P，G分别在边AB，BC，CD，DA上，点M，F，Q都在对角线BD上，且四边形MNPQ和AEFG均为正方形，则
的值等于 ．
参考答案：
【答案】
【解析】试题分析：根据辅助线的性质得到∠ABD=∠CBD=45°，四边形MNPQ和AEFG均为正方形，推出△BEF与△BMN是等腰直角三角形，于是得到FE=BE=AE=
AB，BM=MN=QM，同理DQ=MQ，即可得到结论．
在正方形ABCD中， ∵∠ABD=∠CBD=45°， ∵四边形MNPQ和AEFG均为正方形，
∴∠BEF=∠AEF=90°，∠BMN=∠QMN=90°， ∴△BEF与△BMN是等腰直角三角形，
∴FE=BE=AE=AB，BM=MN=QM， 同理DQ=MQ，
，
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠ACB=
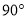，D为AC上一点，DE⊥AB于点E，AC=12，BC=5．
（1）求
的值；（2）当
时，求
的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】两块等腰直角三角形纸片AOB和COD按图1所示放置，直角顶点重合在点O处，AB=25，CD=17．保持纸片AOB不动，将纸片COD绕点O逆时针旋转α（0°<α<90°）角度，如图2所示．
（1）利用图2证明AC=BD且AC⊥BD；
（2）当BD与CD在同一直线上（如图3）时，求AC的长和α的正弦值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】“五一”期间，小明一家乘坐高铁前往某市旅游，计划第二天租用新能源汽车自驾出游． 根据以上信息，解答下列问题：
（1）设租车时间为x小时，租用甲公司的车所需费用为y1元，租用乙公司的车所需费用为y2元，分别求出y1 ， y2关于x的函数表达式；
（2）请你帮助小明计算并选择哪个出游方案合算． -
科目： 来源： 题型：
查看答案和解析>>【题目】把多项式ax2﹣4axy+4ay2分解因式的结果为_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若等腰三角形的一个内角是68°，则顶角是( )
A. 68° B. 44° C. 68°或44° D. 68°或112°
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,AB为⊙O的直径,BC、AD是⊙O的切线,过O点作EC⊥OD，EC交BC于C,交直线AD于E．
（1）求证：CD是⊙O的切线；
（2）若AE=1，AD=3，求阴影部分的面积．
相关试题
