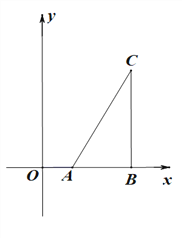
【题目】已知A(2,0),B(6,0),CB⊥x轴于点B,连接AC
画图操作:
(1)在y正半轴上求作点P,使得∠APB=∠ACB(尺规作图,保留作图痕迹)
理解应用:
(2)在(1)的条件下,
①若tan∠APB ![]() ,求点P的坐标
,求点P的坐标
②当点P的坐标为 时,∠APB最大
拓展延伸:
(3)若在直线y![]() x+4上存在点P,使得∠APB最大,求点P的坐标
x+4上存在点P,使得∠APB最大,求点P的坐标
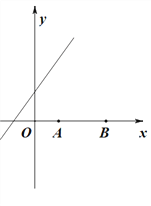
参考答案:
【答案】(1)图形见解析(2)(0,2),(0,4)(0,2![]() )(3)(
)(3)(![]() ,
,![]() )
)
【解析】试题分析:(1)以AC为直径画圆交y轴于P,连接PA、PB,∠PAB即为所求;
(2)①由题意AC的中点K(4,4),以K为圆心AK为半径画圆,交y轴于P和P′,易知P(0,2),P′(0,6);
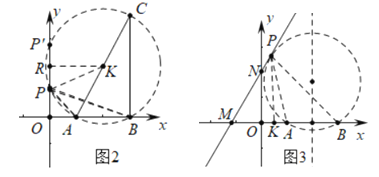
②当⊙K与y轴相切时,∠APB的值最大,(3)如图3中,当经过AB的园与直线相切时,∠APB最大.想办法求出点P坐标即可解决问题;
试题解析:解:(1)∠APB如图所示;
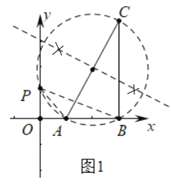
(2)①如图2中,∵∠APB=∠ACB,∴tan∠ACB=tan∠APB=![]() =
=![]() .∵A(2,0),B(6,0),∴AB=4,BC=8,∴C(6,8),∴AC的中点K(4,4),以K为圆心AK为半径画圆,交y轴于P和P′,易知P(0,2),P′(0,6).
.∵A(2,0),B(6,0),∴AB=4,BC=8,∴C(6,8),∴AC的中点K(4,4),以K为圆心AK为半径画圆,交y轴于P和P′,易知P(0,2),P′(0,6).
②当⊙K与y轴相切时,∠APB的值最大,此时AK=PK=4,AC=8,∴BC=![]() =4
=4![]() ,∴C(6,4
,∴C(6,4![]() ),∴K(4,2
),∴K(4,2![]() ),∴P(0,2
),∴P(0,2![]() ).故答案为:(0,2
).故答案为:(0,2![]() ).
).
(3)如图3中,当经过AB的园与直线相切时,∠APB最大.∵直线y=![]() x+4交x轴于M(﹣3,0),交y轴于N(0,4).∵MP是切线,∴MP2=MAMB,∴MP=3
x+4交x轴于M(﹣3,0),交y轴于N(0,4).∵MP是切线,∴MP2=MAMB,∴MP=3![]() ,作PK⊥OA于K.∵ON∥PK,∴
,作PK⊥OA于K.∵ON∥PK,∴![]() =
=![]() =
=![]() ,∴
,∴![]() =
=![]() =
=![]() ,∴PK=
,∴PK=![]() ,MK=
,MK=![]() ,∴OK=
,∴OK=![]() ﹣3,∴P(
﹣3,∴P(![]() ﹣3,
﹣3,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某巡警骑摩托车在一条南北大道上巡逻,某天他从岗亭出发,晚上停留在A处,规定向北方向为正,当天行驶情况记录如下(单位:千米):+10,﹣8,+7,﹣15,+6,﹣16,+4,﹣2
(1)A处在岗亭何方?距离岗亭多远?
(2)若摩托车每行驶1千米耗油0.5升,这一天共耗油多少升?
-
科目: 来源: 题型:
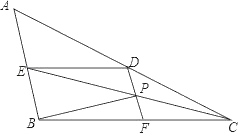
查看答案和解析>>【题目】如图,在△ABC中,CE平分∠ACB交AB于E点,DE∥BC,DF∥AB.
(1)若∠BCE=25°,请求出∠ADE的度数;
(2)已知:BF=2BE,DF交CE于P点,连结BP,AB⊥BP.
①猜想:△CDF的边DF与CD的数量关系,并说明理由;
②取DE的中点N,连结NP.求证:∠ENP=3∠DPN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点D是正方形OABC的边AB上的动点,OC=6.以AD为一边在AB的右侧作正方形ADEF,连结BF交DE于P点.
(1)请直接写出点A、B的坐标;
(2)在点D的运动过程中,OD与BF是否存在特殊的位置关系?若存在,试写出OD与BF的位置关系,并证明;若不存在,请说明理由.
(3)当P点为线段DE的三等分点时,试求出AF的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用同样规格的黑、白两种颜色的正方形瓷砖按下图所示的方式铺宽为1.5米的小路.
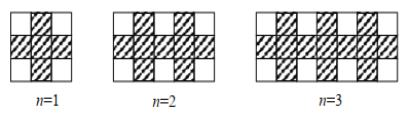
(1)铺第5个图形用黑色正方形瓷砖 块;
(2)按照此方式铺下去,铺第 n 个图形用黑色正方形瓷砖 块;(用含 n的代数式表示)
(3)若黑、白两种颜色的瓷砖规格都为( 长0.5米宽0.5米),且黑色正方形瓷砖每块价格 25 元,白色正方形瓷砖每块价格30元,若按照此方式恰好铺满该小路某一段(该段小路的总面积为 18.75 平方米),求该段小路所需瓷砖的总费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(x1,y1),B(x2,y2),C(x3,y3)在反比例函数y=
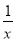 的图象上,若x1<x2<0<x3,则y1,y2,y3的大小关系是( )
的图象上,若x1<x2<0<x3,则y1,y2,y3的大小关系是( )A. y1<y2<y3B. y2<y3<y1C. y3<y2<y1D. y2<y1<y3
-
科目: 来源: 题型:
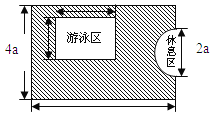
查看答案和解析>>【题目】如图,是一个长方形娱乐场所,其宽是4a米,长是6a米,现要求这个娱乐场拥有一半以上的绿地.小明提供了如图所示的设计方案,其中半圆形休息区和长方形游泳区以外的地方都是绿地,并且半圆形休息区的直径和长方形游泳区的宽都是2a米,游泳区的长3a米.
(1)长方形娱乐场所的面积为 平方米,
休息区的面积为 平方米.
(2)请你判断他的设计方案是否符合娱乐场拥有一半以上的绿地的要求?并说明理由.
(3)若长方形娱乐场所的宽为80米,绿化草地每平方米需要费用20元,求小明设计方案中绿化草地的费用(π取3).
相关试题

