【题目】用同样规格的黑、白两种颜色的正方形瓷砖按下图所示的方式铺宽为1.5米的小路.
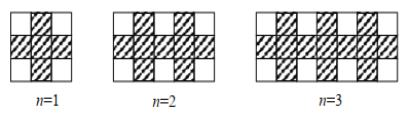
(1)铺第5个图形用黑色正方形瓷砖 块;
(2)按照此方式铺下去,铺第 n 个图形用黑色正方形瓷砖 块;(用含 n的代数式表示)
(3)若黑、白两种颜色的瓷砖规格都为( 长0.5米宽0.5米),且黑色正方形瓷砖每块价格 25 元,白色正方形瓷砖每块价格30元,若按照此方式恰好铺满该小路某一段(该段小路的总面积为 18.75 平方米),求该段小路所需瓷砖的总费用.
参考答案:
【答案】(1)21;(2)4n+1;(3)2005元.
【解析】
(1)根据题意构造出第五个图形的形状,数黑色正方形瓷砖的块数,即可得出答案;
(2)多画几个图形,总结规律,即可得出答案;
(3)分别求出黑白两种瓷砖的块数,乘以各自的价格即可得出答案.
解:(1)由题意可得,铺第5个图形用黑色正方形瓷砖21块;
(2)铺第1个图形用黑色正方形瓷砖5块
铺第2个图形用黑色正方形瓷砖9=5+4块
铺第3个图形用黑色正方形瓷砖13=5+4+4块
铺第4个图形用黑色正方形瓷砖17=5+4+4+4块
铺第5个图形用黑色正方形瓷砖21=5+4+4+4+4块
……
∴铺第n个图形用黑色正方形瓷砖5+4(n-1)=4n+1块
故答案为:4n+1.
(3)18.75÷(0.5×0.5)=75(块)
由题意可得,铺第n个图形共用正方形瓷砖9+6(n-1)=6n+3块,铺第n个图形用白色正方形瓷砖4+2(n-1)=2n+2块
6n+3=75,解得:n=12
可知,第12个图形用黑色正方形:4×12+1=49块,用白色正方形:2×12+2=26块
所以总费用=49×25+26×30=2005(元)
答:该段小路所需瓷砖的总费用为2005元.
-
科目: 来源: 题型:
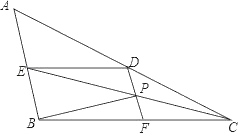
查看答案和解析>>【题目】如图,在△ABC中,CE平分∠ACB交AB于E点,DE∥BC,DF∥AB.
(1)若∠BCE=25°,请求出∠ADE的度数;
(2)已知:BF=2BE,DF交CE于P点,连结BP,AB⊥BP.
①猜想:△CDF的边DF与CD的数量关系,并说明理由;
②取DE的中点N,连结NP.求证:∠ENP=3∠DPN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点D是正方形OABC的边AB上的动点,OC=6.以AD为一边在AB的右侧作正方形ADEF,连结BF交DE于P点.
(1)请直接写出点A、B的坐标;
(2)在点D的运动过程中,OD与BF是否存在特殊的位置关系?若存在,试写出OD与BF的位置关系,并证明;若不存在,请说明理由.
(3)当P点为线段DE的三等分点时,试求出AF的长度.

-
科目: 来源: 题型:
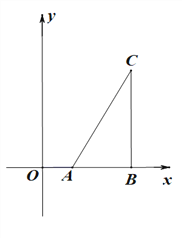
查看答案和解析>>【题目】已知A(2,0),B(6,0),CB⊥x轴于点B,连接AC
画图操作:
(1)在y正半轴上求作点P,使得∠APB=∠ACB(尺规作图,保留作图痕迹)
理解应用:
(2)在(1)的条件下,
①若tan∠APB
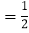 ,求点P的坐标
,求点P的坐标②当点P的坐标为 时,∠APB最大
拓展延伸:
(3)若在直线y
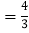 x+4上存在点P,使得∠APB最大,求点P的坐标
x+4上存在点P,使得∠APB最大,求点P的坐标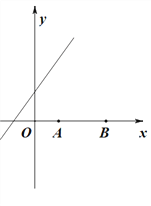
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(x1,y1),B(x2,y2),C(x3,y3)在反比例函数y=
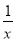 的图象上,若x1<x2<0<x3,则y1,y2,y3的大小关系是( )
的图象上,若x1<x2<0<x3,则y1,y2,y3的大小关系是( )A. y1<y2<y3B. y2<y3<y1C. y3<y2<y1D. y2<y1<y3
-
科目: 来源: 题型:
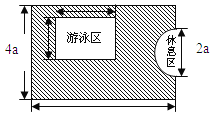
查看答案和解析>>【题目】如图,是一个长方形娱乐场所,其宽是4a米,长是6a米,现要求这个娱乐场拥有一半以上的绿地.小明提供了如图所示的设计方案,其中半圆形休息区和长方形游泳区以外的地方都是绿地,并且半圆形休息区的直径和长方形游泳区的宽都是2a米,游泳区的长3a米.
(1)长方形娱乐场所的面积为 平方米,
休息区的面积为 平方米.
(2)请你判断他的设计方案是否符合娱乐场拥有一半以上的绿地的要求?并说明理由.
(3)若长方形娱乐场所的宽为80米,绿化草地每平方米需要费用20元,求小明设计方案中绿化草地的费用(π取3).
-
科目: 来源: 题型:
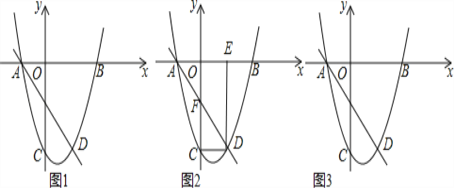
查看答案和解析>>【题目】如图1,直线AD对应的函数关系式为y=﹣2x﹣2,与抛物线交于点A(在x轴上),点D.抛物线与x轴另一交点为B(3,0),抛物线与y轴交点C(0,﹣6).
(1)求抛物线的解析式;
(2)如图2,连结CD,过点D作x轴的垂线,垂足为点E,直线AD与y轴交点为F,若点P由点D出发以每秒1个单位的速度沿DE边向点E移动,1秒后点Q也由点D出发以每秒3个单位的速度沿DC,CO,OE边向点E移动,当其中一个点到达终点时另一个点也停止移动,点P的移动时间为t秒,当PQ⊥DF时,求t的值;(图3为备用图)
(3)如果点M是直线BC上的动点,是否存在一个点M,使△ABM中有一个角为45°?如果存在,直接写出所有满足条件的M点坐标;如果不存在,请说明理由.
相关试题

