【题目】如图,已知:AB∥CD,不添加辅助线,试再添加一个条件,使∠1=∠2成立. 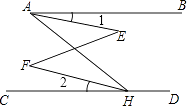
(1)写出两个答案;
(2)选择其中一个加以证明.
参考答案:
【答案】
(1)解:AE∥FH;∠EAH=∠FHA;∠E=∠F(写出两个即可)
(2)解:选择:AE∥FH.
证明:因为AB∥CD,
所以∠BAH=∠CHA,
又因为AE∥FH,
所以∠EAH=∠FHA,
所以∠BAH﹣∠EAH=∠CHA﹣∠FHA,
即∠1=∠2
【解析】根据平行线的性质可得:∠BAH=∠AHC,要使∠1=∠2,只要使∠EAH=∠FHA即可,只要添加AE∥FH即可.
【考点精析】关于本题考查的平行线的判定,需要了解同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图a是一个长为2m、宽为2n的长方形,沿图中实线用剪刀均分成四块小长方形然后按图b的形状拼成一个大正方形.
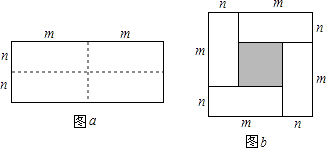
(1)图b中的小正方形的边长等于;
(2)图a中四个长方形的面积和为;图b中四个小长方形的面积和还可以表示为 .
(3)由(2)写出代数式:(m+n)2 , (m﹣n)2 , mn之间的等量关系:;
(4)根据(3)中的等量关系,解决如下问题:若x+y=8,xy=7,则(2x﹣2y)2= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个等腰三角形的两边长分别是5cm和6cm,那么此三角形的周长是
A.15cm B.16cm C.17cm D.16cm或17cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP.
(1)示例:在图1中,通过观察、测量,猜想并写出AB与AP所满足的数量关系和位置关系.
答:AB与AP的数量关系和位置关系分别是 、 .
(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连结AP,BQ.请你观察、测量,猜想并写出BQ与AP所满足的数量关系和位置关系.答:BQ与AP的数量关系和位置关系分别是 、 .
(3)将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连结AP、BQ.你认为(2)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若a3am=a8 , 则m= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(2,﹣5)到x轴、y轴的距离分别为( )
A. 2、5 B. 2、﹣5 C. 5、2 D. ﹣5、2
-
科目: 来源: 题型:
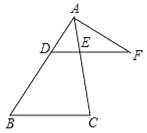
查看答案和解析>>【题目】如图,在△ABC中,点D是AB边上一点,过点D作DE∥BC,交AC于E,点F是DE延长线上一点,联结AF.
(1)如果
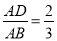 ,DE=6,求边BC的长;
,DE=6,求边BC的长;(2)如果∠FAE=∠B,FA=6,FE=4,求DF的长.
相关试题

