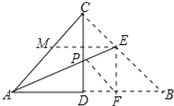
【题目】如图,将一个等腰Rt△ABC对折,使∠A与∠B重合,展开后得折痕CD,再将∠A折叠,使C落在AB上的点F处,展开后,折痕AE交CD于点P,连接PF、EF,下列结论:①tan∠CAE=![]() ﹣1;②图中共有4对全等三角形;③若将△PEF沿PF翻折,则点E一定落在AB上;④PC=EC;⑤S四边形DFEP=S△APF.正确的个数是( )
﹣1;②图中共有4对全等三角形;③若将△PEF沿PF翻折,则点E一定落在AB上;④PC=EC;⑤S四边形DFEP=S△APF.正确的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】C
【解析】试题解析:①正确.作EM∥AB交AC于M.
∵CA=CB,∠ACB=90°,
∴∠CAB=∠CBA=45°,
∵∠CAE=∠BAE=![]() ∠CAB=22.5°,
∠CAB=22.5°,
∴∠MEA=∠EAB=22.5°,
∴∠CME=45°=∠CEM,设CM=CE=a,则ME=AM=![]() a,
a,
∴tan∠CAE=![]() ,故①正确,
,故①正确,
②正确.△CDA≌△CDB,△AEC≌△AEF,△APC≌△APF,△PEC≌△PEF,故②正确,
③正确.∵△PEC≌△PEF,
∴∠PCE=∠PFE=45°,
∵∠EFA=∠ACE=90°,
∴∠PFA=∠PFE=45°,
∴若将△PEF沿PF翻折,则点E一定落在AB上,故③正确.
④正确.∵∠CPE=∠CAE+∠ACP=67.5°,∠CEP=90°﹣∠CAE=67.5°,
∴∠CPE=∠CEP,
∴CP=CE,故④正确,
⑤错误.∵△APC≌△APF,
∴S△APC=S△APF,
假设S△APF=S四边形DFPE,则S△APC=S四边形DFPE,
∴S△ACD=S△AEF,
∵S△ACD=![]() S△ABC,S△AEF=S△AEC≠
S△ABC,S△AEF=S△AEC≠![]() S△ABC,
S△ABC,
∴矛盾,假设不成立.
故⑤错误.
 .
.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】顺次连结矩形四边中点所得的四边形一定是( )
A.菱形
B.矩形
C.正方形
D.等腰梯形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图为放置在水平桌面上的台灯的平面示意图,灯臂AO长为40cm,与水平面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°,求该台灯照亮水平面的宽度BC(不考虑其他因素,结果精确到0.1cm.温馨提示:sin75°≈0.97,cos75°≈0.26,
 ≈1.73).
≈1.73).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰△ABC的顶角∠A=36°(如图).
(1)请用尺规作图法作底角∠ABC的平分线BD,交AC于点D(保留作图痕迹,不要求写作法);
(2)证明:△ABC∽△BDC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列等式从左到右的变形中,属于因式分解的是( )
A.8a2b2 = 2ab4abB.x2-6x=x(x-6)
C.(x+3)2=x2+6x+9D.x2-4+4x=(x+2)( x-2) +4x
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:mn2﹣2mn+m= .
相关试题

