【题目】如图,在半径为2的⊙O中,弦AB长为2.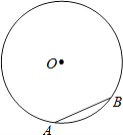
(1)求点O到AB的距离.
(2)若点C为⊙O上一点(不与点A,B重合),求∠BCA的度数.
参考答案:
【答案】
(1)解:过点O作OD⊥AB于点D,连接AO,BO.如图1所示: 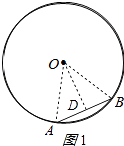
∵OD⊥AB且过圆心,AB=2,
∴AD= ![]() AB=1,∠ADO=90°,
AB=1,∠ADO=90°,
在Rt△ADO中,∠ADO=90°,AO=2,AD=1,
∴OD= ![]() =
= ![]() .
.
即点O到AB的距离为 ![]() .
.
(2)解:如图2所示: 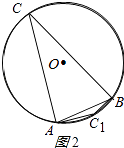
∵AO=BO=2,AB=2,
∴△ABO是等边三角形,
∴∠AOB=60°.
若点C在优弧 ![]() 上,则∠BCA=30°;
上,则∠BCA=30°;
若点C在劣弧 ![]() 上,则∠BCA=
上,则∠BCA= ![]() (360°﹣∠AOB)=150°;
(360°﹣∠AOB)=150°;
综上所述:∠BCA的度数为30°或150°.
【解析】(1)根据题意得到∠ADO=90°,根据勾股定理求出OD的值,即点O到AB的距离;(2)根据题意得到△ABO是等边三角形,∠AOB=60°,根据圆周角与圆心角的关系求出∠BCA的度数为30°或150°.
【考点精析】掌握圆周角定理是解答本题的根本,需要知道顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次
第二次
第三次
第四次
第五次
第六次
平均成绩
中位数
甲
10
8
9
8
10
9
9
①
乙
10
7
10
10
9
8
②
9.5
(1)完成表中填空①;②;
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩方差为 ,你认为推荐谁参加比赛更合适,请说明理由.
,你认为推荐谁参加比赛更合适,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】一只不透明的袋子中,装有三个分别标记为“1”、“2”、“3”的球,这三个球除了标记不同外,其余均相同.搅匀后,从中摸出一个球,记录球上的标记后放回袋中并搅匀,再从中摸出一个球,再次记录球上的标记.
(1)请列出上述实验中所记录球上标记的所有可能的结果;
(2)求两次记录球上标记均为“1”的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图为一位旅行者在早晨8时从城市出发到郊外所走的路程
 单位:千米
单位:千米 与时间
与时间 单位:时
单位:时 的变量关系的图象.根据图象回答问题:
的变量关系的图象.根据图象回答问题: 在这个变化过程中,自变量是______ ,因变量是______ .
在这个变化过程中,自变量是______ ,因变量是______ . 时所走的路程是多少?他休息了多长时间?
时所走的路程是多少?他休息了多长时间? 他从休息后直至到达目的地这段时间的平均速度是多少?
他从休息后直至到达目的地这段时间的平均速度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为创建全国卫生城市,我市某单位全体职工利用周末休息时间参加社会公益活动,并对全体职工参加公益活动的时间
 单位:天
单位:天 进行了调查统计,根据调查结果绘制了如图所示的两幅不完整的统计图,根据信息回答下列问题:
进行了调查统计,根据调查结果绘制了如图所示的两幅不完整的统计图,根据信息回答下列问题: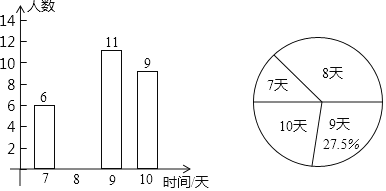
 该单位职工共有______名;
该单位职工共有______名; 补全条形统计图;
补全条形统计图; 职工参加公益活动时间的众数是______天,中位数是______天;
职工参加公益活动时间的众数是______天,中位数是______天; 职工参加公益活动时间总计达到多少天?
职工参加公益活动时间总计达到多少天? -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)

(2)

(3)

(4)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2﹣2x﹣3.
(1)该二次函数图象的对称轴为;
(2)判断该函数与x轴交点的个数,并说明理由;
(3)下列说法正确的是(填写所有正确说法的序号)
①顶点坐标为(1,﹣4);
②当y>0时,﹣1<x<3;
③在同一平面直角坐标系内,该函数图象与函数y=﹣x2+2x+3的图象关于x轴对称.
相关试题

