【题目】已知△ABC的内切圆⊙O与AB、BC、AC分别相切于点D、E、F,若 ![]() =
= ![]() ,如图1,.
,如图1,.
(1)判断△ABC的形状,并证明你的结论;
(2)设AE与DF相交于点M,如图2,AF=2FC=4,求AM的长.
参考答案:
【答案】
(1)
解:△ABC为等腰三角形,
∵△ABC的内切圆⊙O与AB、BC、AC分别相切于点D、E、F,
∴∠CFO=∠CEO=∠BDO=∠BEO=90°,
∵四边形内角和为360°,
∴∠EOF+∠C=180°,∠DOE+∠B=180°,
∵ ![]() =
= ![]() ,
,
∴∠EOF=∠DOE,
∴∠B=∠C,AB=AC,
∴△ABC为等腰三角形;
(2)
解:连接OB、OC、OD、OF,如图,
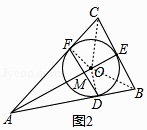
∵等腰三角形ABC中,AE⊥BC,
∴E是BC中点,BE=CE,
∵在Rt△AOF和Rt△AOD中, ![]() ,
,
∴Rt△AOF≌Rt△AOD,
∴AF=AD,
同理Rt△COF≌Rt△COE,CF=CE=2,
Rt△BOD≌Rt△BOE,BD=BE,
∴AD=AF,BD=CF,
∴DF∥BC,
∴ ![]() =
= ![]() =
=![]() ,
,
∵AE= ![]() =4
=4 ![]() ,
,
∴AM=4 ![]() ×
× ![]() =
= ![]() .
.
【解析】(1)易证∠EOF+∠C=180°,∠DOE+∠B=180°和∠EOF=∠DOE,∠B=∠C,AB=AC,即可解题.
(2)连接OB、OC、OD、OF,易证AD=AF,BD=CF可得DF∥BC,根据平行线所截线段成比例;再根据AE长度即可解题.
【考点精析】根据题目的已知条件,利用勾股定理的概念和三角形的内切圆与内心的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心.
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形ABCD中,E、F分别是AD、BC的中点,CE、AF分别交BD于G、H两点.
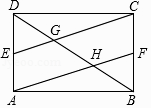
求证:
(1)四边形AFCE是平行四边形;
(2)证明:EG=FH. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两运动员的射击成绩(靶心为10环)统计如下表(不完全):
次数
运动员1
2
3
4
5
甲
10
8
9
10
8
乙
10
9
9
a
b
某同学计算出了甲的成绩平均数是9,方差是
S甲2=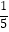 [(10﹣9)2+(8﹣9)2+(9﹣9)2+(10﹣9)2+(8﹣9)2]=0.8,请作答:
[(10﹣9)2+(8﹣9)2+(9﹣9)2+(10﹣9)2+(8﹣9)2]=0.8,请作答:
(1)在图中用折线统计图将甲运动员的成绩表示出来;
(2)若甲、乙射击成绩平均数都一样,则a+b=;
(3)在(2)的条件下,当甲比乙的成绩较稳定时,请列举出a、b的所有可能取值,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级10个班级师生举行毕业文艺汇演,每班2个节目,有歌唱与舞蹈两类节目,年级统计后发现唱歌类节目数比舞蹈类节目数的2倍少4个.
(1)九年级师生表演的歌唱与舞蹈类节目数各有多少个?
(2)该校七、八年级师生有小品节目参与,在歌唱、舞蹈、小品三类节目中,每个节目的演出平均用时分别是5分钟、6分钟、8分钟,预计所有演出节目交接用时共花15分钟,若从20:00开始,22:30之前演出结束,问参与的小品类节目最多能有多少个? -
科目: 来源: 题型:
查看答案和解析>>【题目】以菱形ABCD的对角线交点O为坐标原点,AC所在的直线为x轴,已知A(﹣4,0),B(0,﹣2),M(0,4),P为折线BCD上一动点,作PE⊥y轴于点E,设点P的纵坐标为a.

(1)求BC边所在直线的解析式;
(2)设y=MP2+OP2 , 求y关于a的函数关系式;
(3)当△OPM为直角三角形时,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】若x+5>0,则( )
A.x+1<0
B.x﹣1<0
C.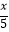 <﹣1
<﹣1
D.﹣2x<12 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1.把△ABC分别绕直线AB和BC旋转一周,所得几何体的地面圆的周长分别记作l1 , l2 , 侧面积分别记作S1 , S2 , 则( )
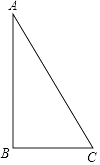
A.l1:l2=1:2,S1:S2=1:2
B.l1:l2=1:4,S1:S2=1:2
C.l1:l2=1:2,S1:S2=1:4
D.l1:l2=1:4,S1:S2=1:4
相关试题

