【题目】如图,直线l1:y1=![]() x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.
x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.
(1)求两直线交点D的坐标;
(2)求△ABD的面积;
(3)根据图象直接写出y1>y2时自变量x的取值范围.

参考答案:
【答案】(1)D点坐标为(4,3)(2)15;(3)x<4
【解析】试题分析:(1)先得到两函数的解析式,组成方程组解求出D的坐标;(2)由y2=![]()
x+1可知,C点坐标为(0,1),分别求出△ABC和△ACD的面积,相加即可.(3)由图可直接得出y1>y2时自变量x的取值范围.
试题解析:(1)将A(0,6)代入y1=![]() x+m得,m=6;将B(-2,0)代入y2=kx+1得,k=
x+m得,m=6;将B(-2,0)代入y2=kx+1得,k=![]()
组成方程组得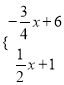 解得
解得![]() 故D点坐标为(4,3);
故D点坐标为(4,3);
(2)由y2=![]() x+1可知,C点坐标为(0,1),S△ABD=S△ABC+S△ACD=
x+1可知,C点坐标为(0,1),S△ABD=S△ABC+S△ACD=![]() ×5×2+
×5×2+![]() ×5×4=15;
×5×4=15;
(3)由图可知,在D点左侧时,y1>y2,即x<4时,出y1>y2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市销售一种饮料,平均每天可售出100箱,每箱利润120元.天气渐热,为了扩大销售,增加利润,超市准备适当降价.据测算,若每箱饮料每降价1元,每天可多售出2箱.针对这种饮料的销售情况,请解答以下问题:
(1)当每箱饮料降价20元时,这种饮料每天销售获利多少元?
(2)在要求每箱饮料获利大于80元的情况下,要使每天销售饮料获利14400元,问每箱应降价多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )

A. 在AC、BC两边高线的交点处
B. 在AC、BC两边中线的交点处
C. 在AC、BC两边垂直平分线的交点处
D. 在∠A、∠B两内角平分线的交点处
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店去年8月底购进了一批文具1160件,预计在9月份进行试销.购进价格为每件10元.若售价为12元/件,则可全部售出.若每涨价0.1元.销售量就减少2件.
(1)求该文具店在9月份销售量不低于1100件,则售价应不高于多少元?
(2)由于销量好,10月份该文具进价比8月底的进价每件增加20%,该店主增加了进货量,并加强了宣传力度,结果10月份的销售量比9月份在(1)的条件下的最低销售量增加了m%,但售价比9月份在(1)的条件下的最高售价减少
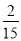 m%.结果10月份利润达到3388元,求m的值(m>10).
m%.结果10月份利润达到3388元,求m的值(m>10). -
科目: 来源: 题型:
查看答案和解析>>【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过
 km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方
km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方 m处,过了2s后,测得小汽车与车速检测仪间距离为
m处,过了2s后,测得小汽车与车速检测仪间距离为 m,这辆小汽车超速了吗?
m,这辆小汽车超速了吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)9(y+4)2﹣49=0
(2)2x2+3=7x(配方法);
(3)2x2﹣7x+5=0 (公式法)
(4)x2=6x+16
(5)2x2﹣7x﹣18=0
(6)(2x﹣1)(x+3)=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划购买甲、乙两种树苗共1000株用以绿化校园,甲种树苗每株25元,乙种树苗每株30元,通过调查了解,甲,乙两种树苗成活率分别是90%和95%.
(1)若购买这种树苗共用去28000元,则甲、乙两种树苗各购买多少株?
(2)要使这批树苗的总成活率不低于92%,则甲种树苗最多购买多少株?
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低?并求出最低费用.
相关试题

