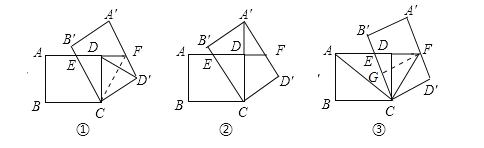
【题目】如图,在矩形ABCD中,AB=3,BC=4,将矩形ABCD绕点C按顺时针方向旋转α角,得到矩形A'B'C'D',B'C与AD交于点E,AD的延长线与A'D'交于点F.

(1)如图①,当α=60°时,连接DD',求DD'和A'F的长;
(2)如图②,当矩形A'B'CD'的顶点A'落在CD的延长线上时,求EF的长;
(3)如图③,当AE=EF时,连接AC,CF,求ACCF的值.
参考答案:
【答案】(1)DD′=3,A′F= 4﹣![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)①如图①中,∵矩形ABCD绕点C按顺时针方向旋转α角,得到矩形A'B'C'D',只要证明△CDD′是等边三角形即可解决问题;
②如图①中,连接CF,在Rt△CD′F中,求出FD′即可解决问题;
(2)由△A′DF∽△A′D′C,可推出DF的长,同理可得△CDE∽△CB′A′,可求出DE的长,即可解决问题;
(3)如图③中,作FG⊥CB′于G,由S△ACF=![]() ACCF=
ACCF=![]() AFCD,把问题转化为求AFCD,只要证明∠ACF=90°,证明△CAD∽△FAC,即可解决问题;
AFCD,把问题转化为求AFCD,只要证明∠ACF=90°,证明△CAD∽△FAC,即可解决问题;
试题解析:(1)①如图①中,∵矩形ABCD绕点C按顺时针方向旋转α角,得到矩形A'B'C'D',∴A′D′=AD=B′C=BC=4,CD′=CD=A′B′=AB=3∠A′D′C=∠ADC=90°,∵α=60°,∴∠DCD′=60°,∴△CDD′是等边三角形,∴DD′=CD=3.
②如图①中,连接CF.∵CD=CD′,CF=CF,∠CDF=∠CD′F=90°,∴△CDF≌△CD′F,∴∠DCF=∠D′CF=![]() ∠DCD′=30°,在Rt△CD′F中,∵tan∠D′CF=
∠DCD′=30°,在Rt△CD′F中,∵tan∠D′CF=![]() ,∴D′F=
,∴D′F=![]() ,∴A′F=A′D′﹣D′F=4﹣
,∴A′F=A′D′﹣D′F=4﹣![]() .
.
(2)如图②中,在Rt△A′CD′中,∵∠D′=90°,∴A′C2=A′D′2+CD′2,∴A′C=5,A′D=2,∵∠DA′F=∠CA′D′,∠A′DF=∠D′=90°,∴△A′DF∽△A′D′C,∴![]() ,∴
,∴![]() ,∴DF=
,∴DF=![]() ,同理可得△CDE∽△CB′A′,∴
,同理可得△CDE∽△CB′A′,∴![]() ,∴
,∴![]() ,∴ED=
,∴ED=![]() ,∴EF=ED+DF=
,∴EF=ED+DF=![]() .
.
(3)如图③中,作FG⊥CB′于G.,∵四边形A′B′CD′是矩形,∴GF=CD′=CD=3,∵S△CEF=![]() EFDC=
EFDC=![]() CEFG,∴CE=EF,∵AE=EF,∴AE=EF=CE,∴∠ACF=90°,∵∠ADC=∠ACF,∠CAD=∠FAC,∴△CAD∽△FAC,∴
CEFG,∴CE=EF,∵AE=EF,∴AE=EF=CE,∴∠ACF=90°,∵∠ADC=∠ACF,∠CAD=∠FAC,∴△CAD∽△FAC,∴![]() ,∴AC2=ADAF,∴AF=
,∴AC2=ADAF,∴AF=![]() ,∵S△ACF=
,∵S△ACF=![]() ACCF=
ACCF=![]() AFCD,∴ACCF=AFCD=
AFCD,∴ACCF=AFCD=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不能使两个直角三角形全等的条件( )
A. 一条直角边及其对角对应相等
B. 斜边和一条直角边对应相等
C. 斜边和一锐角对应相等
D. 两个锐角对应相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列条件中,不能判定两直角三角形全等的是( )
A. 斜边和一锐角对应相等
B. 斜边上的中线和一直角边对应相等
C. 两边分别相等
D. 直角的平分线和一直角边对应相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE,DE,DC.
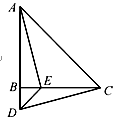
(1)求证:△ABE≌△CBD;
(2)若∠CAE=30°,求∠BDC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】从同一张底片上冲出来的两张五寸照片________全等图形,从同一张底片上冲出来的一张一寸照片和一张两寸照片________全等图形(填“是”或“不是”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠A=20°,∠B=27°,AC⊥DE,求∠1,∠D的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式组
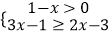 的解集在数轴上表示为 ( )
的解集在数轴上表示为 ( )
A.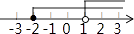
B.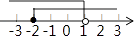
C.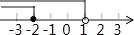
D.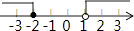
相关试题

