【题目】如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
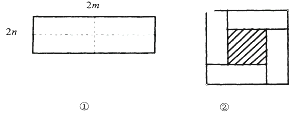
(1)你认为图②中的阴影部分的正方形的边长等于_________________.
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积.
方法①_________________________________________________________.
方法②_________________________________________________________.
(3)观察图②,你能写出(m+n)2,(m-n)2,mn这三个代数式间的等量关系吗?
参考答案:
【答案】(1)、m-n;(2)、(m-n)2;(m+n)2-4mn;(3)、(m-n)2=(m+n)2-4mn
【解析】(1)根据①可得图②中的阴影部分的正方形的边长等于m-n;
(2)根据长方形和正方形的面积公式以及图形可得图②中阴影部分的面积是:(m+n)2-4mn或(m-n)2;
(3)根据②可直接得出(m+n)2-4mn=(m-n)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】包装厂有42名工人,每人平均每天可以生产圆形铁片120片或长方形铁片80片.为了每天生产的产品刚好制成一个密封的圆桶,应该分配多少名工人生产圆形铁片,多少名工人生产长方形铁片?设应分配x名工人生产长方形铁片,(42-x)名工人生产圆形铁片,则下列所列方程正确的是( )
A. 120x=2×80(42-x) B. 80x=120(42-x)
C. 2×80x=120(42-x) D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD的对角线AC、BD相交于点O,E,F分别是OA,OC的中点,连接BE,DF
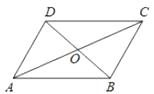
(1)根据题意,补全原形;
(2)求证:BE=DF. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解本校九年级男生“引体向上”项目的训练情况,随机抽取该年级部分男生进行了一次测试(满分15分,成绩均记为整数分),并按测试成绩(单位:分)分成四类:A类(12≤m≤15),B类(9≤m≤11),C类(6≤m≤8),D类(m≤5)绘制出以下两幅不完整的统计图,请根据图中信息解答下列问题:

(1)本次抽取样本容量为 , 扇形统计图中A类所对的圆心角是度;
(2)请补全统计图;
(3)若该校九年级男生有300名,请估计该校九年级男生“引体向上”项目成绩为C类的有多少名? -
科目: 来源: 题型:
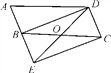
查看答案和解析>>【题目】如图,将□ABCD的边AB延长至点E,使AB=BE,连接BD,DE,EC,DE交BC于点O.
(1)求证:△ABD≌△BEC;
(2)若∠BOD=2∠A,求证:四边形BECD是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:五莲县新玛特购物中心第一次用5000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的
 倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价) 甲
乙
进价(元/件)
20
30
售价(元/件)
29
40
(1)新玛特购物中心将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该购物中心第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB∥DC,∠B=90°,F为DC上一点,且FC=AB,E为AD上一点,EC交AF于点G.
(1)求证:四边形ABCF是矩形;
(2)若ED=EC,求证:EA=EG.

相关试题

