【题目】以线段AC为对角线的凸四边形ABCD(它的四个顶点A、B、C、D按顺时针方向排列,每个内角均小于180°),已知AB=BC=CD,∠ABC=120°,∠CAD=30°,则∠BCD的大小为____________.
参考答案:
【答案】60°或120°
【解析】
∵AB=BC, ∠ABC=120°,
∴∠1=∠2=∠CAD=30°,
∴AD∥BC,
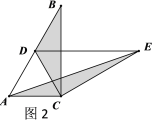
如图1,过点C分别作CE⊥AB于E,CF⊥AD于F,
∵∠1=∠CAD,
∴CE=CF,
在Rt△ACE与Rt△ACF中,
∵AC=AC,
CE=CF,
∴Rt△ACE≌Rt△ACF,
∴∠ACE=∠ACF,
在Rt△BCE与Rt△DCF中,
∵CB=CD,
CE=CF,
∴Rt△BCE≌Rt△DCF,
∴∠BCE=∠DCF,
∴∠2=∠ACD=30°,
∴∠BCD=60°;
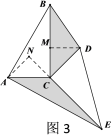
如图2,

∵AD∥BC,AB=CD′,
∴四边形ABCD′是等腰梯形,
∴∠BCD′=∠ABC=120°.
所以∠BCD=60°或120°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列关于x的方程有实数根的是( )
A.x2﹣x+1=0
B.x2+x+1=0
C.(x﹣1)(x+2)=0
D.(x﹣1)2+1=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】某服装厂生产一种夹克和T恤,夹克每件定价100元,T恤每件定价60元,厂方在开展促销活动期间,向客户提供两种优惠方案:①买一件夹克送一件T恤 ②夹克和T恤都按定价的8折付款.
现某客户要到该服装厂购买夹克30件,T恤x件(x>30).
(1)若按方案①购买夹克和T恤共需 元(用含x的式子表示),若按方案②购买夹克和T恤共需 元(用含x的式子表示)
(2)若x=40,通过计算说明按方案①,②,哪种方案购买较为合算?
(3)当购买多少件T恤时,按以上两种方案购买所付价钱一样多?
-
科目: 来源: 题型:
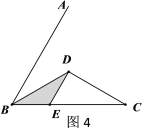
查看答案和解析>>【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B =∠E=30°.
(1)操作发现
如图2,固定△ABC,使△DEC绕点C旋转.当点D恰好落在AB边上时,填空:
 线段DE与AC的位置关系是 ;
线段DE与AC的位置关系是 ; 设△BDC的面积为
设△BDC的面积为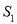 ,△AEC的面积为
,△AEC的面积为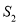 ,则
,则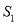 与
与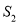 的数量关系是 .
的数量关系是 .(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中
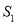 与
与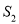 的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高DM和AN,请你证明小明的猜想.
的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高DM和AN,请你证明小明的猜想.(3)拓展探究
已知∠ABC=60°,点D是其角平分线上一点,BD=CD=4,DE∥AB交BC于点E(如图4).若在射线BA上存在点F,使
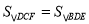 ,请求出相应的BF的长.
,请求出相应的BF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠α的余角是48°,则∠α的补角为_____度.
-
科目: 来源: 题型:
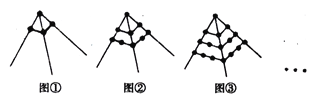
查看答案和解析>>【题目】探索与推断:
(1)有四个数,把其中每三个数相加,其和分别为22,24,27,20.求这四个数分别为多少?
(2)观察下列图形中的点的个数,若按其规律再画下去:
①请你画出第4个图形,并指出第4个图形中的点的个数;
②第n个图形中所有点的个数是多少?(用含n的代数式表示)
③若图形中共有1600个点,则该图是第几个图形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC≌△DEF,AB=DE,∠A=70°,∠E=30°,则∠F的度数为()
A. 80° B. 70° C. 30° D. 100°
相关试题

