【题目】△ABC中,AD是BC边上的高,BD=3,CD=1,AD=2,P、Q、R分别是BC、AB、AC边上的动点,则△PQR周长的最小值为
参考答案:
【答案】![]()
【解析】解:如图1中,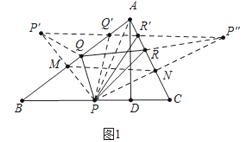
作P点关于AB的对称点P′,作P点关于AC的对称点P″,连接P′P″,与AB交于点Q′,与AC交于点R′,连接PP′交AB于M,连接PP″交AC于N,
此时△PQ′R′的周长最小,这个最小值=P′P″,
∵PM=MP′,PN=NP″,
∴P′P″=2MN,
∴当MN最小时P′P″最小.
如图2中,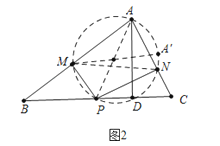
∵∠AMP=∠ANP=90°,
∴A、M、P、N四点共圆,线段AP就是圆的直径,MN是弦,
∵∠MAN是定值,
∴直径AP最小时,弦MN最小,
∴当点P与点D重合时,PA最小,此时MN最小.
如图3中,
∵在RT△ABD中,∠ADB=90°,AD=2,DB=3,
∴![]()
在RT△ADC中,∵∠ADC=90°,AD=2,CD=1,
∴![]()
∵DM⊥AB,DN⊥AC,
∴![]() ACDN=
ACDN=![]() DCAD,
DCAD,
∴![]()
∵∠MAD=∠DAB,∠AMD=∠ADB,
∴△AMD∽△ADB,
∴![]()
∴AD2=AMAB,同理AD2=ANAC,
∴AMAB=ANAC,
∴![]()
∵∠MAN=∠CAB,
∴△AMN∽△ACB,
∴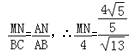
∴MN=![]() ,
,
∴△PQR周长的最小值=P′P″=2MN=![]() .
.
故答案为![]() .
.
如图1中,作P点关于AB的对称点P′,作P点关于AC的对称点P″,连接P′P″,与AB交于点Q′,与AC交于点R′,连接PP′交AB于M,连接PP″交AC于N,此时△PQ′R′的周长最小,这个最小值=P′P″,再证明P′P″=2MN,MN最小时,△PQR周长最小,利用图2证明当点P与点D重合时MN最小,在图3中利用相似三角形的性质求出MN的最小值即可解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一根绳子对折成线段AB,从点P处把绳子剪断,已知AP:BP=2:3,若剪断后的各段绳子中最长的一段为60 cm,求绳子的原长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1.有位学生写出了以下五个结论:
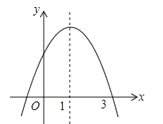
(1)ac>0;
(2)方程ax2+bx+c=0的两根是x1=﹣1,x2=3;
(3)2a﹣b=0;
(4)当x>1时,y随x的增大而减小;
则以上结论中正确的有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
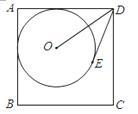
查看答案和解析>>【题目】如图,⊙O与正方形ABCD的两边AB、AD相切,且DE与⊙O相切于E点.若正方形ABCD的周长为44,且DE=6,则sin∠ODE=
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,O是AC上一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形且
 ,求∠B的大小.
,求∠B的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.当∠MAN绕点A旋转到BM=DN时(如图1),易证BM+DN=MN.

(1)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM,DN和MN之间有怎样的数量关系?写出猜想,并加以证明.
(2)当∠MAN绕点A旋转到如图3的位置时,线段BM,DN和MN之间又有怎样的数量关系?请直接写出你的猜想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:tan260°+4sin30°cos45°
(2)解方程:x2﹣4x+3=0.
相关试题

